|
twinbee
|
 |
« Reply #30 on: March 15, 2010, 11:34:18 PM » |
|
msltoe, wow that looks amazingly close to the holy grail we're looking for - and probably the best so far. Congrats!
Can you zoom in to the 'equivalent' of seahorse valley on one of those sphere-lets at say 10-50 iterations?
|
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #31 on: March 16, 2010, 03:04:39 PM » |
|
All, Thanks for the compliments. This is an interesting and encouraging discovery, but the crown jewel has yet to be discovered. Twinbee: I don't think zooming in this Julia set will bring anything exciting. If you consider the 2-D Julia variant, the zooming in just brings in more and more smaller bulbs, with no mixing of antennae-like structures. One interesting application of this "mirroring" method is that it produces more aesthetically pleasing 3-D Julia set renderings by removing the z=+/-1 poles. The mirroring is continuous, but not analytic. I experimented with some variants to fix the squashing of the bulbs that start in the x=0 plane. Here's the latest formula: if (z*z<y*y) { r = x*x+y*y+z*z+4*y*y*z*z; r1 = sqrt(r); theta = 2*atan2(y,x); phi = 2*asin(z/r1); r = x*x+y*y+z*z; x1 = r*cos(theta)*cos(phi); y1 = r*sin(theta)*cos(phi); z1 = -r*sin(phi); } else { r = x*x+y*y+z*z+4*y*y*z*z; r1 = sqrt(r); theta = 2*atan2(z,x); phi = 2*asin(y/r1); r = x*x+y*y+z*z; x1 = r*cos(theta)*cos(phi); y1 = -r*sin(phi); z1 = r*sin(theta)*cos(phi); } x=x1+a;y=y1+b;z=z1+c; The Julia variant (-0.8,0,0) looks a little less distorted than the previous one: 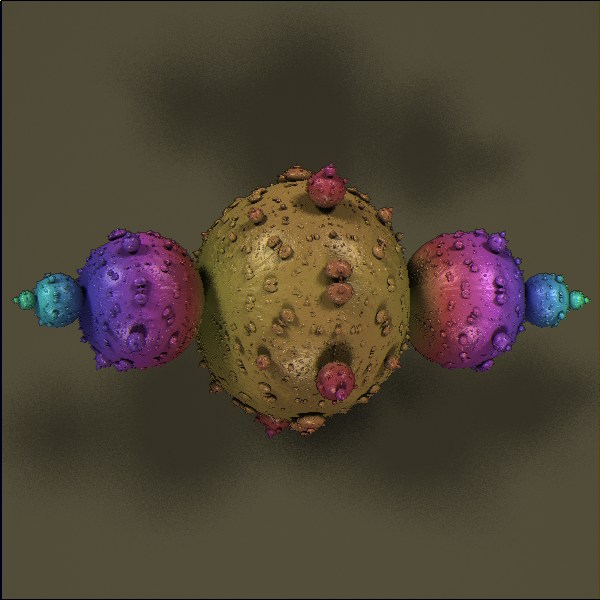 But the M-set lacks the beauty and symmetry of the J-set: 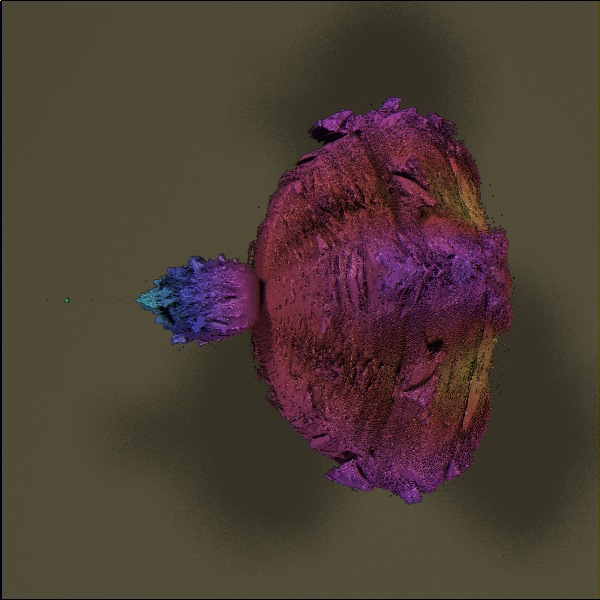 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #32 on: March 16, 2010, 04:01:27 PM » |
|
It's not all that bad, actually  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
matsoljare
|
 |
« Reply #33 on: March 16, 2010, 08:45:52 PM » |
|
I'd be really interested in seeing a "julibrot" projection of that last one....
|
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #34 on: March 17, 2010, 04:18:35 PM » |
|
Ok. so maybe I'm getting a little carried away with symmetry operations, but this 8-fold variant fills the spherical surface better than the 4-fold. I've done higher n-folds, but they're less exotic. There's something really strange about how the translational (a,b,c) field (aka Mandelbrot formula) works in 3-d space. Once we figure this out, the "true" 3-D Mandelbrot should be within reach. 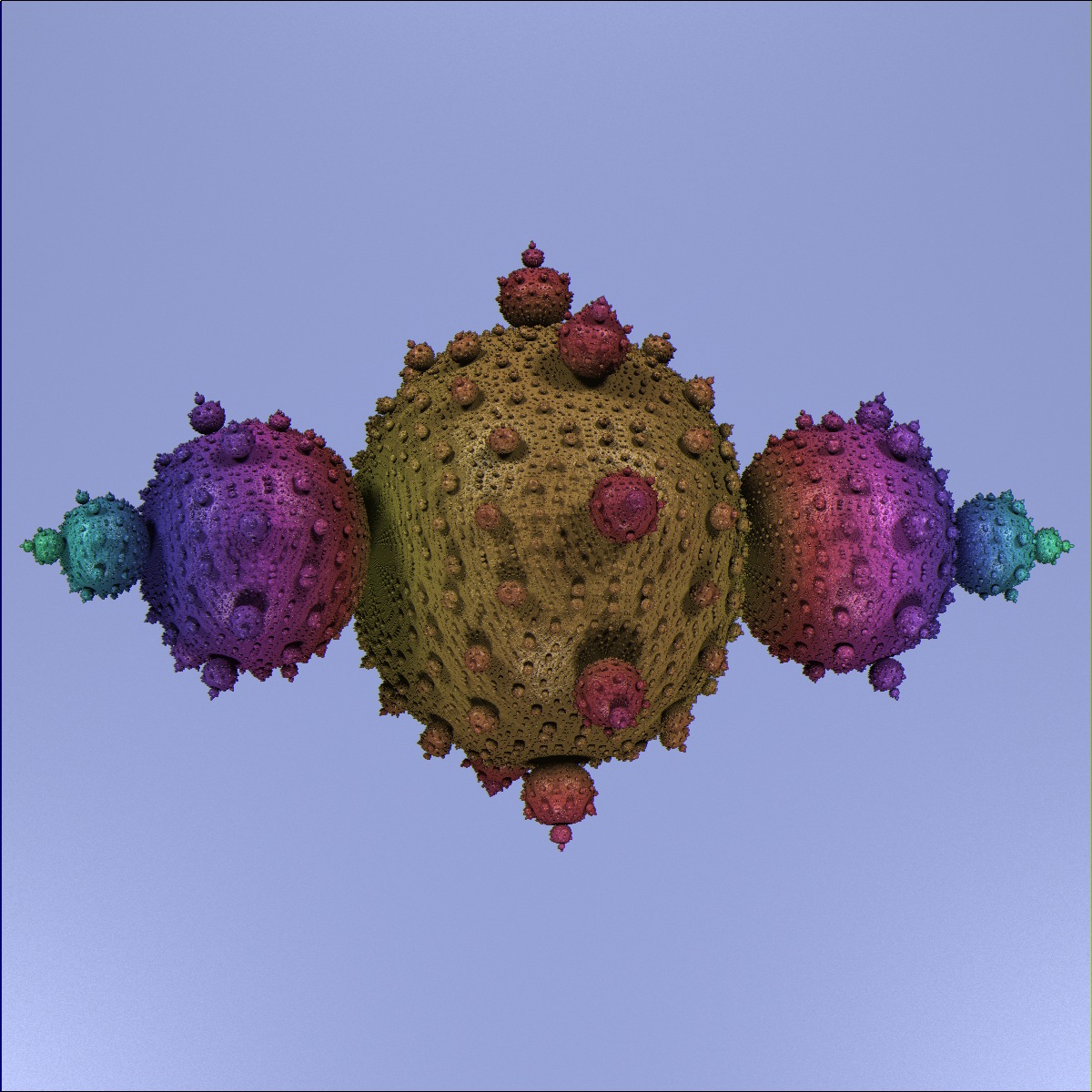 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
KRAFTWERK
|
 |
« Reply #35 on: March 17, 2010, 04:48:33 PM » |
|
It's surreal!, but almost everything here is  I like it a lot anyway... |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #36 on: March 17, 2010, 05:18:57 PM » |
|
For the M-set, if only the y-z behavior could be fixed, we'd be set. Although, this has been the problem since day 1.
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #37 on: March 18, 2010, 03:03:04 PM » |
|
Spectacular! Wow, how close is that? Distortion on the spheres is either fixed, or very minimal for the smaller spheres maybe.
EDIT: Wouldn't mind seeing it with a lower iteration...
|
|
|
|
« Last Edit: March 18, 2010, 06:37:00 PM by twinbee »
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #38 on: March 18, 2010, 06:51:15 PM » |
|
Lower iterations are very different than Mbulbs in that they are not bulbous, rather look more like a low iteration 2D Mset. I'll try to get a pic posted tonight.
|
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #39 on: March 19, 2010, 12:52:45 AM » |
|
Various maximum iterations. My numbering scheme may be off by 1:  The code: psi = atan2(z,y)+pi*2; psi2 = 0; while (psi > pi/8) { psi -= pi/4; psi2 -= pi/4; } cs = cos(psi2); sn = sin(psi2); y1 = y*cs-z*sn; z1 = y*sn+z*cs; y = y1; z = z1; x1 = (x*x-y*y)*(1-z*z/(x*x+y*y+z*z)); y1 = (2*x*y)*(1-z*z/(x*x+y*y+z*z)); z1 = 2*z*sqrt(x*x+y*y); y = y1*cs+z1*sn; z = -y1*sn+z1*cs; x=x1-0.8; y=y+0; z=z+0; Note the slight change in the Mandelbulb equation which seems to cause less distortion, also z1 can be positive or negative yet produces the same Julia set. |
|
|
|
« Last Edit: March 19, 2010, 12:59:28 AM by msltoe »
|
 Logged
Logged
|
|
|
|
|
KRAFTWERK
|
 |
« Reply #40 on: March 19, 2010, 08:55:49 AM » |
|
N=5 is nice, it's like it is struggling to get out of its shell... More iterations please, I want to get OUT!!!  |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #41 on: March 20, 2010, 03:26:47 AM » |
|
Because of my success with the Julia variant, I've been obsessed on cracking the code using symmetry operations to cull out the right stuff. I've found three M-set variants so far. The following is the closest hit, but still a far way off. The general idea is to vary between + and - rsin(phi) over even and odd iterations. The 16-fold symmetry was done for a specific reason. The un-symmetrized version has a little bulb in a small angular span. The symmetry operation was used to extract that out but discard the boring stuff. I conjecture that the real M3D, if it exists, requires minimal or no symmetrizing.  I'm using a very high number of iterations (N=200). If you dial that down, you lose the smooth bulbs. But, maybe, there would be less fuzz and more of something to discern when zooming in. The bulbs look promising from a distance, but upon zooming in lack the symmetry seen in the Julia set. |
|
|
|
« Last Edit: March 20, 2010, 03:37:51 AM by msltoe »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #42 on: March 20, 2010, 01:21:11 PM » |
|
That looks nice  What about distance estimation?  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #43 on: March 20, 2010, 05:21:07 PM » |
|
It keeps getting closer! Good for you on not giving up - the Mandelbulb would look like a barren desert compared to the delights we can expect if you found it. I agree that one wouldn't think any symmetry operations to be needed. Actually, I wonder if you could zoom into these areas highlighted by red boxes - we could already start to be seeing some strange and wonderful things. EDIT: Just read your end quote. To be honest, I'd still like to see some zoom-ins to the earlier Julia version. I know the Julia has less interesting detail than the Mandelbrot equivalent generally, but I'm still curious  |
|
|
« Last Edit: March 20, 2010, 05:42:53 PM by twinbee »
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #44 on: March 21, 2010, 02:42:01 AM » |
|
Twinbee, KRAFTWERK, kram1032, ...: I appreciate your encouragement as I stumble away. I also believe that a true 3-d mandelbrot will have incredible complexity to explore for years to come. Right now, you could say I'm simulating what we think it should look like, which ultimately will help us visualize and find the real result. Twinbee: I'm constantly modifying the formulas , so I haven't had a chance to do too many zooms, but I zoomed into the minibrot that you suggested and sure enough it looks a bit different than its parent:  I've also done some zooms of the Julia x8 set which do actually show a bit of complexity mainly, I think, because I'm not using the exact formula. This is one I posted in the gallery a few days ago: 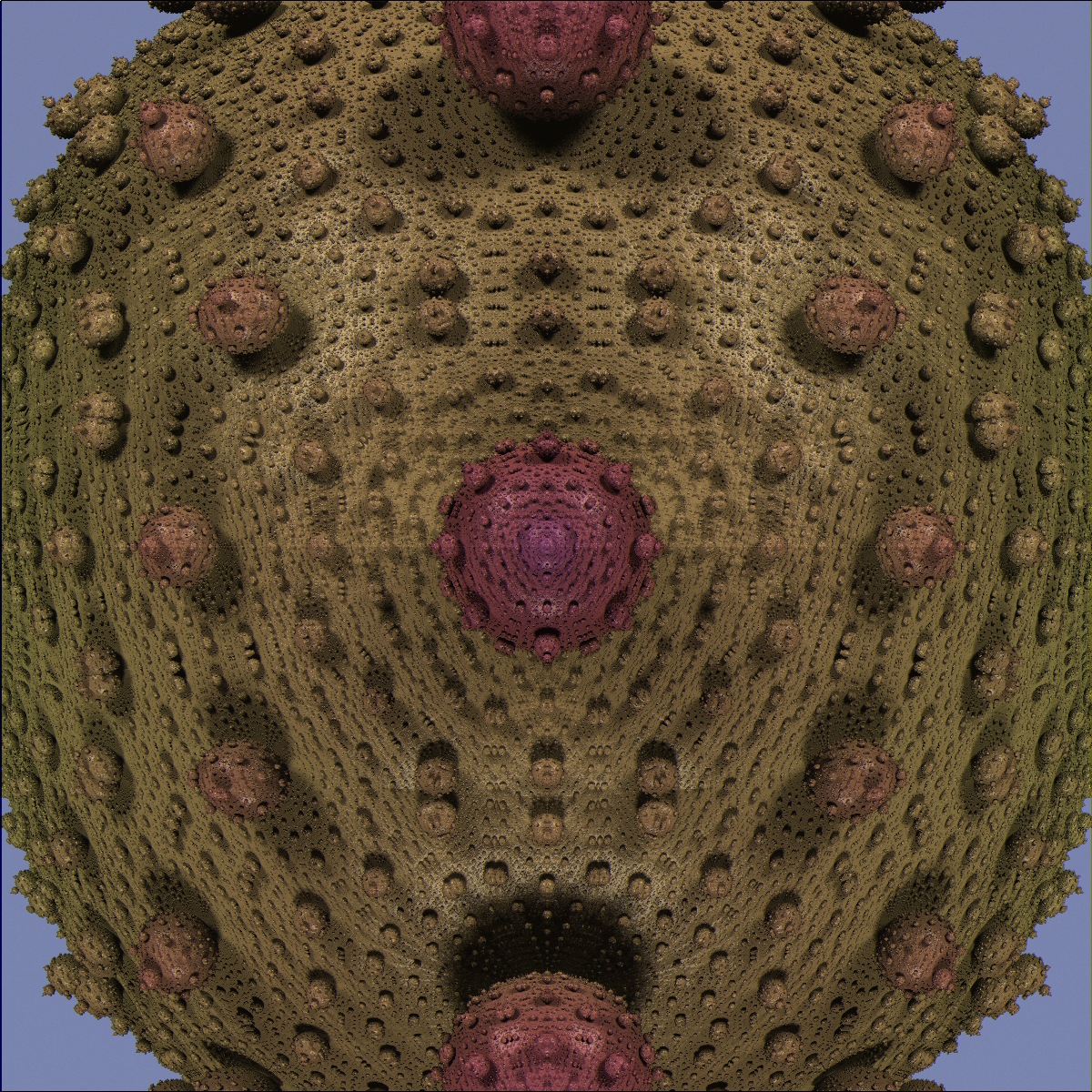 I shared that formula so anyone can pursue it. It would make a nice movie. -mike |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















