|
kram1032
|
 |
« Reply #15 on: January 24, 2010, 03:31:19 AM » |
|
this one actually looks like it might be worth for a zoom...  |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #16 on: January 25, 2010, 03:05:33 AM » |
|
I truncated the norm by mistake on the last picture. If you let the fractal reach its true extent it has some disconnected flowers. I also added some color... finally. No more "all blues." Not sure if zooming would bring out much as there may be some non-isotropic stretching.
|
|
|
« Last Edit: January 25, 2010, 03:20:44 AM by msltoe »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #17 on: January 25, 2010, 02:10:52 PM » |
|
nice, however, the colours are so saturate that they actually kill some detail...  |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #18 on: January 25, 2010, 02:42:12 PM » |
|
kram1032: It's not the colors' fault, I think. The un-truncated fractal doesn't have the "furriness" of the truncated one. Instead, there's a lot of thin flakes like the first icosahedral one I showed. It seems that radial scaling is too fast compared to attraction to the vertices.
|
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #19 on: February 08, 2010, 04:22:53 AM » |
|
With my updated rendering code, here's the fractal from the first post revisited. Some flat parts and some chaos. Algorithm: if ((x*x>y*y)&&(x*x>z*z)) { x1 = x*x-y*y-z*z; y1 = 2*x*y; z1 = 2*x*z; } if ((y*y>z*z)&&(y*y>x*x)) { x1 = 2*x*y; y1 = y*y-x*x-z*z; z1 = 2*y*z; } if ((z*z>y*y)&&(z*z>x*x)) { x1 = 2*x*z; y1 = 2*y*z; z1 = z*z-x*x-y*y; } x = x1+a;y=y1+b;z=z1+c; 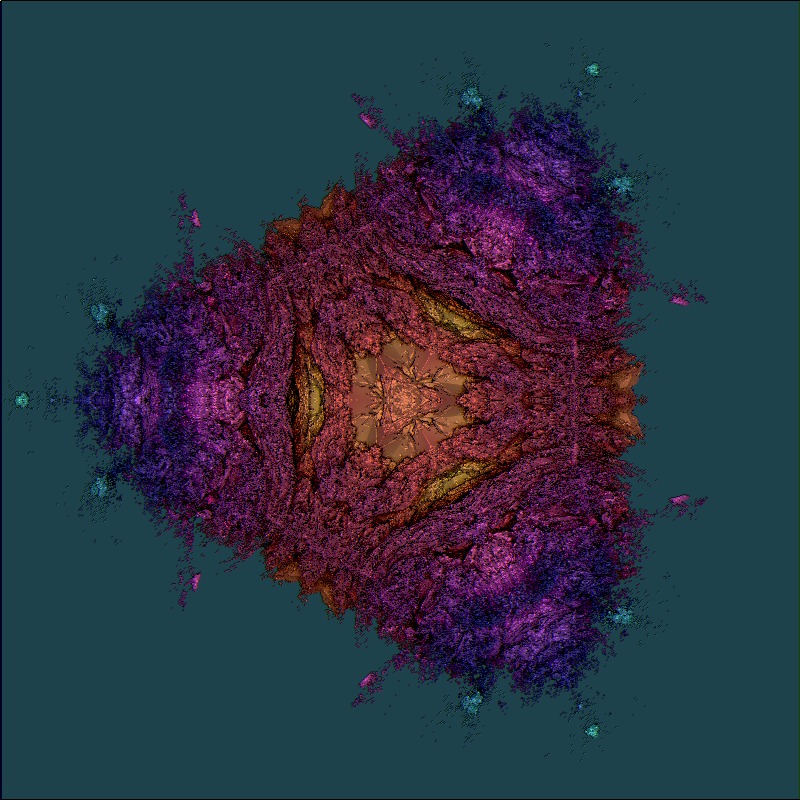   |
|
|
|
« Last Edit: February 08, 2010, 04:30:05 AM by msltoe »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #20 on: February 08, 2010, 03:03:48 PM » |
|
Nice  You know, even if that what you said before was the case, hyper-saturate colours tend to kill some amounts of details... THe new renders with less saturation are way better with that  |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #21 on: February 09, 2010, 02:53:11 AM » |
|
kram1032: There's a balance of saturation vs. detail. I guess I find the bright colors appealing, reminds me of candy. Here's the 6-way attractor rendered with better methods:  Ignore the diagonal line going through the center. That must be an artifact of my "if" statements. :  |
|
|
|
« Last Edit: February 09, 2010, 02:54:58 AM by msltoe »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #22 on: February 09, 2010, 03:49:49 PM » |
|
With some nice organometallic textures, those could be the merge of nature and technology, when on one had the robots get intelligent enough and on the other hand nature fights back and they suddenly notice that both have the same goals and start a symbiosis O.o Ok, I guess I have too much fantasy today  Anyways, very nice and somewhat cuborganic  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #23 on: February 11, 2010, 05:45:51 AM » |
|
By request, the icosahedral attractor. I found a simple shortcut instead of computing the rotated quaternion attractors. The idea is that z^2 can also be thought of as a reflection of the pole [e.g.,(1,0,0)] to (x,y,z) with lots of sphere normalizations.
Actually reminds me of virus capsids which somebody attempted to render for me in a koch snowflake form. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #24 on: March 15, 2010, 03:04:27 PM » |
|
Using a Mandelbub order 2 transformation with interchange of y and z depending on z*z < or > y*y, the Julia with seed (-0.75,0,0) has some nice bulb properties. Essentially, the interchange removes the poles, but introduces some discontinuities at |y| = |z|. Careful examination suggests the true 3-D Mandelbrot is stil elusive. For example, the bulbs get squashed in the y-z plane.  |
|
|
|
« Last Edit: March 15, 2010, 03:06:55 PM by msltoe »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #25 on: March 15, 2010, 03:15:02 PM » |
|
that's VERY close  How does the whole Mset of this look like? |
|
|
|
|
 Logged
Logged
|
|
|
|
msltoe
Iterator

Posts: 187
|
 |
« Reply #26 on: March 15, 2010, 03:25:28 PM » |
|
The M-set of this one is actually the Mandellettuce I posted several months earlier on this thread.
Julias look better in some cases even though (I think) they tend to be more self-similar and less diverse as you zoom in.
I'll try to get a new pic of the M-set of this one tomorrow, but as you'll see it's very much lacking.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
KRAFTWERK
|
 |
« Reply #27 on: March 15, 2010, 04:30:29 PM » |
|
Cool, mandel-pumpkin?  Very interesting! |
|
|
|
|
 Logged
Logged
|
|
|
|
hobold
Fractal Bachius

Posts: 573
|
 |
« Reply #28 on: March 15, 2010, 05:29:00 PM » |
|
Careful examination suggests the true 3-D Mandelbrot is stil elusive. You certainly got very close. I have wondered myself if Tglad's folding trick could somehow be used on the sphere to let any poles vanish during a Mandelbulb computation. But even then the coordinate system would still introduce some distortion. |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #29 on: March 15, 2010, 11:14:17 PM » |
|
Very cool msltoe  |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















