|
Buddhi
|
 |
« on: November 11, 2010, 02:21:12 PM » |
|
Because as Trifox said people, this thread is growing too large, are you ok if i close it, with notice for next thread ?
" True 3D mandelbrot fractal (search for the holy grail continues)" is so long, I'm starting new thread for continuing this endless quest Last days I decided to experiment with rotations in Mandelbulb formula. I tried to do some formula with no privileged axis. In standard Mandelbulb formula there are two rotations. First around Z axis and second around axis which is perpendicular to plane created by z axis and resultant vector of x and y vectors. So X axis is privileged. In my version of formula I used 3 simple rotations. First around Z axis, second around Y axis and third around X axis. There is a code is below: double rp = pow(r, p-1);
double angZ = atan2(z.y, z.x);
double angY = atan2(z.z, z.x);
double angX = atan2(z.z, z.y);
CRotationMatrix rotM;
rotM.RotateX(angX*(p-1));
rotM.RotateY(angY*(p-1));
rotM.RotateZ(angZ*(p-1));
z = rotM.RotateVector(z) * rp + constant;
r = z.Length(); Results are not as beautiful as standard Mandelbulb but bulbs also exists in all directions. Example of power 2 version:  Example of power 5 vesion with cross-sections:  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #1 on: November 11, 2010, 03:25:19 PM » |
|
it is like the definition of paolo bonzini, and i also think that the coordinate axis can be any orientation, in the base bulb functions there is the y axis mirrored, so the rotation appears clockwise, instead of counter clockwise, i had an axis angle variant in my mind, you define 2 axis to which the polar coordinates or calculated, and proceed as usual, the matrices gets a bit more complicated, but can be created once for a whole image, also rotating around 3 axis makes sense, to squeeze out maximum transformation  nice images |
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
Buddhi
|
 |
« Reply #2 on: November 13, 2010, 05:41:56 PM » |
|
Some new formulas:Two rotations: around Z and Y axis. Rotations are done using complex numbers. First the vector is normalized, next rotated and at the end multipled by inverted normalization factor. I have to use "signum" function, because fist part of formula loses sign of x value. Resultant fractal has 2 symmetries and there is visible 2D Mandelbrot set on slices XY and XZ. double tempR;
double sign = 1.0;
double sign2 = 1.0;
//rotation around Z axis
if (z.x < 0) sign2 = -1.0;
tempR = sqrt(z.x * z.x + z.y * z.y);
z *= (1.0 / tempR);
temp = z.x * z.x - z.y * z.y;
z.y = 2.0 * z.x * z.y;
z.x = temp;
z *= tempR;
//rotation around X axis
if (z.x < 0) sign = -1.0;
tempR = sqrt(z.x * z.x + z.z * z.z);
z *= (1.0 / tempR);
temp = z.x * z.x - z.z * z.z;
z.z = 2.0 * z.x * z.z * sign2;
z.x = temp * sign;
z *= tempR;
z = z * r;
z += constant;
r = z.Length();  XY and XZ slices:  Second formula: Three rotation, also done with complex numbers. Result is weird but some structures are like on xenodreambui's images http://www.fractalforums.com/3d-fractal-generation/true-3d-mandlebrot-type-fractal/msg8246/#msg8246double tempR;
//rotation around Z axis
tempR = sqrt(z.x * z.x + z.y * z.y);
z *= (1.0 / tempR);
temp = z.x * z.x - z.y * z.y;
z.y = 2.0 * z.x * z.y;
z.x = temp;
z *= tempR;
//rotation around X axis
tempR = sqrt(z.y * z.y + z.z * z.z);
z *= (1.0 / tempR);
temp = z.y * z.y - z.z * z.z;
z.z = 2.0 * z.y * z.z;
z.y = temp;
z *= tempR;
//rotation around Y axis
tempR = sqrt(z.x * z.x + z.z * z.z);
z *= (1.0 / tempR);
temp = z.x * z.x - z.z * z.z;
z.z = 2.0 * z.x * z.z;
z.x = temp;
z *= tempR;
z = z * r;
z += constant;
r = z.Length(); 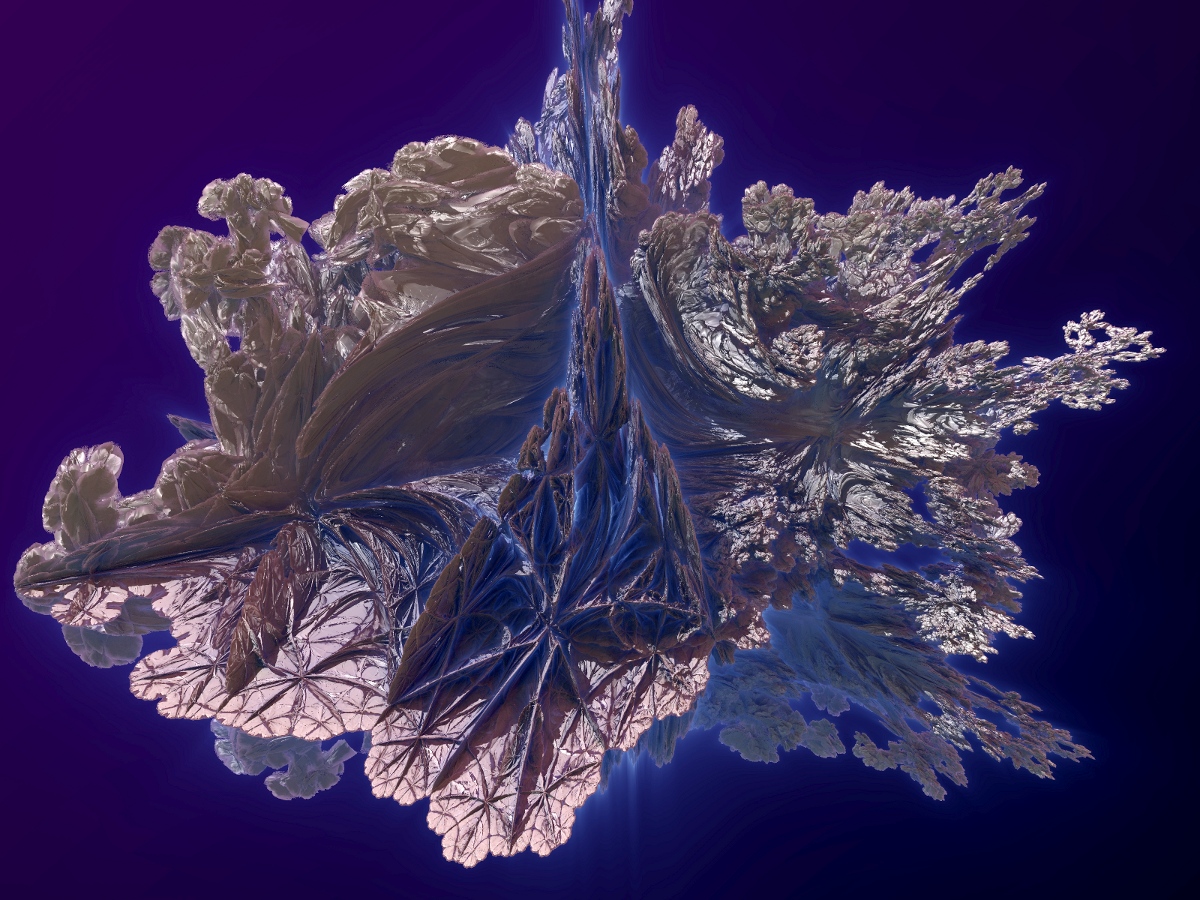 Some zoom:  I have already implemented these formulas in Mandelbulber 0.96
|
|
|
|
|
 Logged
Logged
|
|
|
|
Collin237
Forums Newbie

Posts: 8
|
 |
« Reply #3 on: June 16, 2011, 12:28:38 PM » |
|
Unfortunately, I don't have a program to test this with.
A complex analytic function is a conformal mapping. So I was thinking, instead of looking for a 3D analog of complex numbers, what about simply looking for a 3D conformal mapping, regardless of whether it makes sense algebraically? I'm suggesting the following formula:
x → x² + 2x(y+z) - y² - z² + c1
y → y² + 2y(x+z) - x² - z² + c2
z → z² + 2z(x+y) - x² - y² + c3
If anyone can get an image of this, please let me know.
Thanks, Collin
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #4 on: June 16, 2011, 09:57:15 PM » |
|
Unfortunately, I don't have a program to test this with.
A complex analytic function is a conformal mapping. So I was thinking, instead of looking for a 3D analog of complex numbers, what about simply looking for a 3D conformal mapping, regardless of whether it makes sense algebraically? I'm suggesting the following formula:
x → x² + 2x(y+z) - y² - z² + c1
y → y² + 2y(x+z) - x² - z² + c2
z → z² + 2z(x+y) - x² - y² + c3
If anyone can get an image of this, please let me know.
Thanks, Collin
Here is the fractal rendered from your formula:  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Tater
|
 |
« Reply #5 on: July 13, 2013, 08:31:00 PM » |
|
Because as Trifox said " True 3D mandelbrot fractal (search for the holy grail continues)" is so long, I'm starting new thread for continuing this endless quest Last days I decided to experiment with rotations in Mandelbulb formula. I tried to do some formula with no privileged axis. In standard Mandelbulb formula there are two rotations. First around Z axis and second around axis which is perpendicular to plane created by z axis and resultant vector of x and y vectors. So X axis is privileged. In my version of formula I used 3 simple rotations. First around Z axis, second around Y axis and third around X axis. There is a code is below: double rp = pow(r, p-1);
double angZ = atan2(z.y, z.x);
double angY = atan2(z.z, z.x);
double angX = atan2(z.z, z.y);
CRotationMatrix rotM;
rotM.RotateX(angX*(p-1));
rotM.RotateY(angY*(p-1));
rotM.RotateZ(angZ*(p-1));
z = rotM.RotateVector(z) * rp + constant;
r = z.Length(); ... If I understand correctly, this is rotating the vector around each axis by a multiple of the current angle and using that same multiple for the power of the length. Have you tried rotating around each axis by a constant amount instead, so that, for instance, the vector is rotated by 30 degrees around the x, y and z axes each iterate? Perhaps a power of the length could be different from the constant of rotation too. |
|
|
|
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #6 on: November 26, 2016, 11:33:46 PM » |
|
Those formulas have an immense potential but they were simply forgot since years?  Firstly I must point out that they should be simplified in the normalization part; //rotation around Z axis tempR = 1.0/sqrt(z.x * z.x + z.y * z.y); temp = z.x * z.x - z.y * z.y; z.y = 2.0 * z.x * z.y; z.x = temp; z.xy *= tempR; Does the same as Buddhi's one but just two multiplication vs six. The interesting part? Try to insert some fabs around, anywhere. I dunno how many possible variations you can get but some are really wonderful. Images will come soon  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #7 on: November 27, 2016, 11:38:34 AM » |
|
I have "generalized" the rotating function like this; void Rho(double* u, double* v, int* op)
{
double Rtemp, tempR, temp;
//rotation around any axis; pass them to this function
Rtemp = Hypot(*u,*v); // unused, hypot = sqrt(y^2+x^2)
tempR = recip(Rtemp); // 1/arg
double uu = *u, vv = *v;
if (*op & 8) uu = fabs(uu);
if (*op & 16) vv = fabs(vv);
temp = uu * *u - vv * *v;
if (*op & 4) temp = fabs(temp);
uu = *u; vv = *v;
if (*op & 1) uu = fabs(uu);
if (*op & 2) vv = fabs(vv);
*v = uu * vv; *v += *v;
*u = temp;
*u *= tempR; *v *= tempR;
return;
} Where you let the user choose an integer as op, op can go 0 to 31 for each rotation; total of 32^3 = 32768  variations, some very nice some very distorted.  If all user params are zero you get the normal thingy.  It gives burning ship, celtic and normal mandelbrot for the xy slice, but the xz slice is always fuzzy at least for the triple rotation version. Pictures now.  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #8 on: November 27, 2016, 12:28:59 PM » |
|
... (Here I disabled the YZ rotation, as it incredibly increases fuzziness & seems to piss off Mandel)  |
No sweat, guardian of wisdom!
|
|
|
|
Sabine
|
 |
« Reply #9 on: November 27, 2016, 01:04:49 PM » |
|
 There really is too much to try and experiment with! 
|
|
|
|
|
 Logged
Logged
|
sabine62.deviantart.com
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #10 on: November 27, 2016, 07:03:54 PM » |
|
A grailish Julia set...  Variant (2; NO; 12) (No YZ rot  )  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
M Benesi
|
 |
« Reply #11 on: November 27, 2016, 08:04:28 PM » |
|
combine with: //sr12= sqrt (1/2) sr13= sqrt(1/3).....
tx=z.x*sr23-z.z*sr13; //rotate
z.z=z.x*sr13 + z.z*sr23;
z.x=tx*sr12-z.y*sr12;
z.y=tx*sr12+z.y*sr12;
z=abs(z)*T1Scale; //do thingy and scale t1scale=2
dr*=T1Scale;
tx=z.x*sr12+z.y*sr12; //rotate back and subtract offset from x...
z.y=-z.x*sr12+z.y*sr12;
z.x=tx*sr23+z.z*sr13-T1offset; //t1offset~2?? maybe sqrt(3) if it's after... forgot :D
z.z=-tx*sr13+z.z*sr23;
|
|
|
|
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #12 on: November 27, 2016, 08:48:14 PM » |
|
Matthew images plsss  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
Sabine
|
 |
« Reply #13 on: November 27, 2016, 11:07:33 PM » |
|
A little preview (very slow render!) with XYrot on  |
sabine62.deviantart.com
|
|
|
|

















