|
David Makin
|
 |
« Reply #75 on: May 16, 2010, 04:18:26 AM » |
|
Yes! that's what make them so interresting, but they are not really IFS fractals (in general). There are DE technique For IFS that are not exponential in time (see this article). David Makin have also developped a technique similar to one that is described in that article. Just skimmed that article and would just like to add a comment - to get the probabilities and fractal dimension for an affine system then the correct method is to solve: log(p0)/log(s0) = log(p1)/log(s1) = ........... = log(pn)/log(sn) = fractal dimension Where p0 to pn are the probabilities for transforms 0 to n and s0 to sn are the scales. Obviously it assumes you know the scales - either calculated or estimated. For example for an IFS where all the scales are the same (such as the Menger Sponge) then you can calculate the probability anyway and the dimension reduces to: log(p)/log(s) In the case of the Menger Sponge the probability is 1/20 and the scale is 1/3 giving dimension = log(1/20)/log(1/3) i.e. 2.7268330278608420413960946363642  The above method comes from: "A Multifractal Analysis of IFSP Invariant Measures With Application to Fractal Image Generation" by J.M. Gutierrez and A. Iglesias and M.A. Rodrıguez I don't have the source for the above except that it used to be available on the internet as "fractals96.pdf"  |
|
|
|
« Last Edit: May 16, 2010, 04:20:19 AM by David Makin »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #76 on: May 16, 2010, 03:02:31 PM » |
|
Yes! that's what make them so interresting, but they are not really IFS fractals (in general). There are DE technique For IFS that are not exponential in time (see this article). David Makin have also developped a technique similar to one that is described in that article. Just skimmed that article and would just like to add a comment - to get the probabilities and fractal dimension for an affine system then the correct method is to solve: log(p0)/log(s0) = log(p1)/log(s1) = ........... = log(pn)/log(sn) = fractal dimension Where p0 to pn are the probabilities for transforms 0 to n and s0 to sn are the scales. Obviously it assumes you know the scales - either calculated or estimated. For example for an IFS where all the scales are the same (such as the Menger Sponge) then you can calculate the probability anyway and the dimension reduces to: log(p)/log(s) In the case of the Menger Sponge the probability is 1/20 and the scale is 1/3 giving dimension = log(1/20)/log(1/3) i.e. 2.7268330278608420413960946363642  The above method comes from: "A Multifractal Analysis of IFSP Invariant Measures With Application to Fractal Image Generation" by J.M. Gutierrez and A. Iglesias and M.A. Rodrıguez I don't have the source for the above except that it used to be available on the internet as "fractals96.pdf"  Just to add that the above is directly analagous to the measure theory version of fractal dimension i.e. log(new length)/log(old length) i.e. the probability is analagous to new length and the scale to old length. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #77 on: May 16, 2010, 06:03:41 PM » |
|
I have just done first steps with IFS formula. I used formula proposed by tglad and knighty. I like this formula because is very easy for parametrisation (will be easy to render morph animation). My final (little simplified) version of formula is: point = mRotation.RotateVector(point);
for(int i=0; i<IFSfoldingCount; i++)
{
length = point.Dot(IFSDirection[i]);
if(length > IFSDistance[i])
{
point -= IFSDirection[i]*2.0*(length - IFSDistance[i]);
}
}
point += IFSOffset;
z *= scale; My first image was rendered with following parameters Symmetry vectors: direction 1 = {1.0, 0, 0} direction 2 = {0.5, -0.5, -0.707} direction 3 = {0.5, 0.5, -0,707} distance1 = distance2 = distance3 = 1 scale = 2; offset = {0,0,0}  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #78 on: May 16, 2010, 08:39:35 PM » |
|
This is the most amazing formula I have ever seen!!! I gives almost unlimited possibilities. Thank you for share this. My latest render: Symmetry vectors: s1 = {1.0, 0, -0,5} s2 = {0, 1/sqrt(3), 1/3} s3 = {0, 1/sqrt(3), -1/3} s4 = {-1.0,0,-0.5} scale = 2; offset = {0,0,0} distance1 = distance2 = distance3 = distance4 = 1  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #79 on: May 16, 2010, 11:12:41 PM » |
|
Nice renderings  . Rotating the folding planes and adding the last rotation will give you much more variety. I think you can simplify the folding down to the code I wrote, rotating the point for after each fold should be equivalent to having each subsequent direction vector rotated, and a total rotation at the end. The rotations should also compose down into just 1 rotation.
I realize now that you were right. This is good news because the simplified algorithm is faster. Take three reflection planes in a dodecahedron, one through an edge, one through a diagonal of one of the pentagonal sides and one perpendicular to the said edge. These form a triangle. Changing the scaling point inside that triangle gives, amongst others, the following shapes.
One of them is a soccer ball..the first ever fractal one!
 Looks definetly that 3 planes are sufficient to obtain platonic and regular-polyhedron-sierpinski  . The triangle you described is called the fundamental triangle and the symmetries defined by the planes defined by the edges of that triangle and the origin are in fact the generator set of the group of symmetries of dodecahedron (see Coxeter groups and Wythoff caleidoscopic construction). It should be the same for tetrahedra and octahedra. Good new! I was wrong  . Using the plans defined by the fundamental triangle will give close but different (and interresting) results. Here is the dodeca "siepinski" I obtained:  But I had to do 4 pre folds.(the same iteration but without the stretch). Here is what I obtained with 0,1,2 and 3 pre folds:  I've also tried using only one folding. Here are the results:    In case you are interrested (and have a powerful PC) here are the evaldraw scripts I used for those pictures: Kaleidoscopic IFS experiments.(use 1/4 resolution for near realtime exploration  ) |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #80 on: May 16, 2010, 11:16:49 PM » |
|
picture obtained using non uniform scaling: 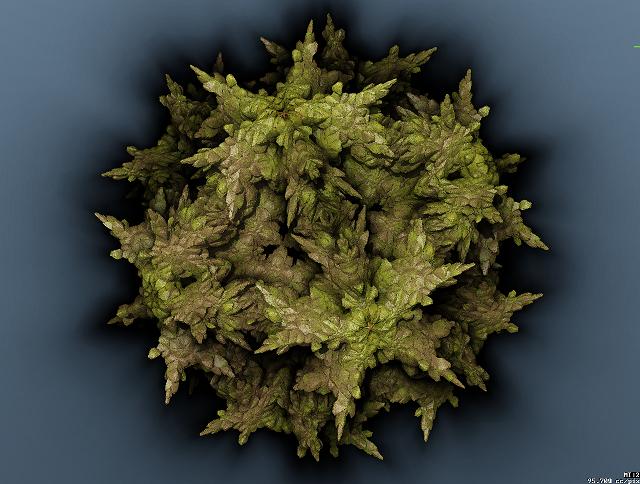 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Hamilton
|
 |
« Reply #81 on: May 16, 2010, 11:42:37 PM » |
|
Well, I can say that this is one of the most interesting thread about IFS fractals I've ever read so far...
Thanks again for sharing this, guys!
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
JosLeys
|
 |
« Reply #82 on: May 17, 2010, 12:13:45 AM » |
|
Knighty, what you have there in that first image is the icosa sierp, not the dodeca.
..and I think there is something wrong with your code, as one should not be able to see the background through it...
Here us what I get (scale=2)
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #83 on: May 17, 2010, 01:15:00 AM » |
|
those results are amazing! So you now directly extended any generic 2D IFS to any generic 3D IFS! Well, any not-tree-like IFS, I guess.... What's about branches like in L-systems? Could they be extended and added in a similar fashion? Maybe a tree with actual thickness could be figured out by using non-uniform scales like the one spiky fractal? And then blend that with a Mandelbulb to get it to have fruits  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
cbuchner1
|
 |
« Reply #84 on: May 17, 2010, 01:39:44 AM » |
|
those results are amazing!
So you now directly extended any generic 2D IFS to any generic 3D IFS!
I agree, this is wonderful. With all the discoveries made during the last 6 months or so (Mandelbulb, Mandelbox, Kaleidoscopic IFS) there is certainly enough material to fill an entire book about the science and the beauty of 3D fractals. What I am desperately missing is some reference material collecting all the formulas in one place. There exists a nice thread summarizing the formulas for different varieties of Mandelbulbs, but I haven't found anything similar for the new varieties of 3D fractals yet. |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #85 on: May 17, 2010, 02:35:34 AM » |
|
Excuse the low res pics, this is a quick variation I tried out, fractal rocks Vector dir = randomDirectionVector()
float dot = point.dot(dir)
float dist = randomFloat0to1()
if (dot > dist)
point -= 2*dir*(dot-dist)
elseif (dot < -dist)
point -= 2*dir*(dot+dist)
point *= 1.15 |
|
|
|
|
|
Softology
|
 |
« Reply #86 on: May 17, 2010, 06:16:01 AM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
cbuchner1
|
 |
« Reply #87 on: May 17, 2010, 09:32:02 AM » |
|
Stop copying nature  Chances are it's patented already by Monsanto. Humor aside, these are most excellent pics! |
|
|
|
|
 Logged
Logged
|
|
|
|
|
KRAFTWERK
|
 |
« Reply #88 on: May 17, 2010, 09:40:54 AM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #89 on: May 17, 2010, 03:07:09 PM » |
|
Knighty, what you have there in that first image is the icosa sierp, not the dodeca.
Oops! sorry, I've always been confused on this  ..and I think there is something wrong with your code, as one should not be able to see the background through it...
Here us what I get (scale=2)
I've checked everything and couldn't spot any error. Here is the code I used (the folding planes are not the same as yours BTW): #define _PHI_ (0.5*(1+sqrt(5)))
static stc[3]={_PHI_,1,0};
#define IN3 (1/sqrt(14+6*sqrt(5)))
static n3[3]={IN3*_PHI_,-IN3*(_PHI_^2),-IN3*(2*_PHI_+1)};
fractal(x,y,z,scale){
for(i=0;i<4;i++){//Pre-fold
y=abs(y);
z=abs(z);
t=x*n3[0]+y*n3[1]+z*n3[2];
if(t<0){x-=2*t*n3[0];y-=2*t*n3[1];z-=2*t*n3[2];}
}
r=x*x+y*y+z*z;
for(i=0;i<MI && r<bailout;i++){//actual iterations
y=abs(y);
z=abs(z);
t=x*n3[0]+y*n3[1]+z*n3[2];
if(t<0){x-=2*t*n3[0];y-=2*t*n3[1];z-=2*t*n3[2];}
x=scale*x-stc[0]*(scale-1);
y=scale*y-stc[1]*(scale-1);
z=scale*z-stc[2]*(scale-1);
r=x*x+y*y+z*z;
}
(sqrt(x*x+y*y+z*z)-2)*scale^(-i)
}
What's about branches like in L-systems? Could they be extended and added in a similar fashion?
Well... I think so, because  : Excuse the low res pics, this is a quick variation I tried out, fractal rocks Vector dir = randomDirectionVector()
float dot = point.dot(dir)
float dist = randomFloat0to1()
if (dot > dist)
point -= 2*dir*(dot-dist)
elseif (dot < -dist)
point -= 2*dir*(dot+dist)
point *= 1.15 |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















