|
|
|
billtavis
|
 |
« Reply #16 on: February 23, 2015, 05:40:01 PM » |
|
LOL yeah it's probably not the best way either.  Claude mentioned above that you could walk away from the set using Newton's method. But I have no idea what that means or how to do it, and thinking in terms of Euler integration is natural to me because a lot of my experience on computers is with simulation-based animations. This article gives a good overview of the integration methods: http://gafferongames.com/game-physics/integration-basics/Basically, I start at a pixel, and get a c-value (it's coordinate location in space). Next I treat that pixel like a particle, and the potential of the mandelbrot set like a velocity field. I "run the simulation" until the "particle" is far enough away from the origin to measure its angle. I'm not sure how else I can elaborate on it. Certainly, I am not going to be able to produce any maths about it. Are there any parts you are having trouble understanding? I'd be happy to clarify. |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #17 on: February 26, 2015, 04:42:09 AM » |
|
And here is a function that uses the getGradeint function to perform Runge-Kutta integration and find the external angle. It's assumed that the point has already been checked for being outside the set. double externalAngle(...) {
...
return (std::atan2(cky,ckx));
}
This gets you the angle in only double-precision, but using double precision floating point throughout it's possible to get the external angle in much higher precision - the trick is to collect bits from the binary representation of the angle as you cross each dwell band - whether the final iterate that escaped has a positive or negative imaginary part determines if the bit is 0 or 1 respectively, see binary decomposition colouring http://www.mrob.com/pub/muency/binarydecomposition.html . This is orthogonal to using Newton's method - it should also work with your potential field particle simulation technique as long as you never skip more than one dwell band at a time. The idea behind Newton's method is to gradually reduce your target potential keeping the angle fixed to find a target final-z value, then solve for c in f^n(0, c) = z-final using the current c-value as initial guess for Newton's method iterations. The amount you reduce the potential by is controlled by a parameter called "sharpness", essentially the number of steps to take within each dwell band - usually I use between 4 and 8. This means the number of steps taken is known in advance (sharpness * initial dwell) and usually you don't need many Newton's method iterations to converge at each step (around 2 - 5 was typical in some tests I did a while ago). You can only decrease potential so much for a fixed n with a fixed escape radius, so eventaully you decrement n, which increases |z-final| and gives you a choice of two angles (the pre-images under angle doubling) for arg z-final, you pick the one which is closer to the n'th iterate of your current c value, and which one you pick also tells you another bit of the external angle). The algorithm is described here, for the other direction (starting from an external angle and tracing inwards to the Mandelbrot set - it's simpler because there is only one image under angle-doubling instead of two possibilities for the inverse): http://www.math.nagoya-u.ac.jp/~kawahira/programs/mandel-exray.pdfI have a few implementations, the currently maintained ones are: external ray tracing inwards (double precision floating point, libgmp arbitrary precision rational for external angle) https://gitorious.org/mandelbrot/mandelbrot-numerics/source/3d55cfc99cc97decb0ba0d9c2fb271a504b8e504:c/lib/m_d_exray_in.chttp://code.mathr.co.uk/mandelbrot-numerics/blob/72eeac97a15f6c8c5f06be4b82bcf63d17c4851e:/c/lib/m_d_exray_in.cexternal ray tracing outwards (double precision floating point, libgmp arbitrary precision rational for external angle) https://gitorious.org/mandelbrot/mandelbrot-numerics/source/3d55cfc99cc97decb0ba0d9c2fb271a504b8e504:c/lib/m_d_exray_out.chttp://code.mathr.co.uk/mandelbrot-numerics/blob/72eeac97a15f6c8c5f06be4b82bcf63d17c4851e:/c/lib/m_d_exray_out.cexternal ray tracing inwards (libmpfr arbitrary precision floating point, libgmp arbitrary precision rational for external angle) https://gitorious.org/mandelbrot/mandelbrot-numerics/source/3d55cfc99cc97decb0ba0d9c2fb271a504b8e504:c/lib/m_r_exray_in.chttp://code.mathr.co.uk/mandelbrot-numerics/blob/72eeac97a15f6c8c5f06be4b82bcf63d17c4851e:/c/lib/m_r_exray_in.cexternal ray tracing outwards (libmpfr arbitrary precision floating point, libgmp arbitrary precision rational for external angle) (still to be implemented) |
|
|
|
« Last Edit: March 10, 2015, 02:26:21 AM by claude, Reason: gitorious.org is closing »
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #18 on: February 27, 2015, 12:51:05 PM » |
|
I adapted billtavis' code to collect bits. First I changed the getGradient function to return the continuous iteration count and the sign of the last iterate: void getGradient(long double cx, long double cy, long double &xDer,
long double &yDer, long double &gzx, long double &gzy,
long double &length, unsigned int maxIter,
long double &m, bool &b) { // these two are the new ones
...
b = zy < 0 || (zy == 0 && zx < 0);
m = n + 1 - std::log2(std::log(length) / (0.5 * std::log(huge)));
...
}
I used a different formula for m, because I had issues with the original (but they only differ by a constant factor and offset afaict) - the one I use has integer spacing of dwell bands and m = 2 for |c| = sqrt(huge) = escape radius. I also wrote a wrapper without the extra arguments, that just calls the one with extra arguments, so I didn't have to change so much code in externalAngle(). Then I added bit collection in externalAngle(): typedef std::vector<bool> BITS;
BITS externalAngle(long double cx, long double cy, size_t maxIter, long double &e) { // returns a vector of bits, atan2 result in e
...
long double m = maxIter * 2;
long double m_old = m;
BITS bs;
bool b;
while (m_old > 2) { // this replaces the previous while loop start
getGradient(ckx,cky,xDer,yDer,gzxA,gzyA,length,maxIter, m, b);
if (std::ceil(m) < m_old) { // collect a bit if we crossed a dwell band
bs.push_back(b);
m_old = m;
}
...
dist = std::min(std::max(16.0L, 0.01 * std::sqrt(ckx * ckx + cky * cky)),0.5*dist); // replaces the previous clamping, 16 is a tiny step size with very large |c|
... // rest of loop body unchanged
}
e = (std::atan2(cky,ckx));
reverse(bs.begin(), bs.end()); // the bits were collected least-significant first
return bs;
}
Then there's the main program which takes command line arguments, converts the atan2 result from long double to a vector of bits, compares it with the (hopefully more accurate) vector of bits result, and prints them out. See the attached source code file for details. Here are some tests, which seem to indicate the atan2 result is valid to about 16 bits, even though long double has 64 bits of mantissa precision: $ # cre cim iter # pre(periodic) angle of nearby landing point
$ ./tavis 0.251 0 1000 # .(0)
.0000000000000000000000000000000000000000000000000000000000000000
.0000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000
$ ./tavis -2.001 0 1000 # .1(0)
.100000000000 0000000000000000000000000000000000000000000000000000
.100000000000
$ ./tavis -0.75 0.01 1000 # .(01)
.01010101010101001 01000001111000101111100010001010101110101011011
.01010101010101010 1010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101001001111
$ ./tavis 1e-16 1 1000 # .0(01)
.0010101010101001 111110001001100001110001111010000110100110001111
.0010101010101010 101010101010101010101010101100100111011
$ ./tavis -1.749 1e-10 1000 # .(011)
.01101101101100 00100000101001101000000110000110110110011010111011
.01101101101101 101101101101101101101101101101001001001001001001001001001001001100100100101001110001
$ ./tavis -1.01 0.251 1000 # .(01011001)
.010110010101011 1001111010111001000000101111001011001111100001000
.010110010101100 101011001010110010101100101011001010110010101100101011001010110100100111111
$ ./tavis -0.99 0.251 1000 # .(01010110)
.01010110010101011 00111001100111100010010001110011010011101111011
.01010110010101100 1010110010101100101011001010110010101100101011001010110010101010110100011101
|
|
|
|
 Logged
Logged
|
|
|
|
|
billtavis
|
 |
« Reply #19 on: March 02, 2015, 10:14:55 PM » |
|
wow!  Thanks Claude, your new way of measuring the angle is great! I've had some impressive preliminary results... I will post some pictures once I get a few more kinks worked out. |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #20 on: March 03, 2015, 11:55:58 AM » |
|
 You can get a longer bitstring by starting with the binary representation of the argument of the first escaped iterate of the initial point (must use the same escape radius), instead of an empty bitstring. See updated code attached. Refering to the image in http://www.fractalforums.com/index.php?topic=20866.0 the bit collection gets one bit per vertical dwell band going upwards, but you can use the horizontal position within the lowest cell too - billtavis' original algorithm effectively only uses the horizontal cell position once the ray gets to the top. EDIT: I just fixed a bug in the code (missing 'else' around line 173), attachment replaced... |
|
|
« Last Edit: March 03, 2015, 12:47:17 PM by claude, Reason: code bugfix »
|
 Logged
Logged
|
|
|
|
|
billtavis
|
 |
« Reply #21 on: March 04, 2015, 07:33:41 PM » |
|
soo... I did lots of tests... here's some results... Here's a closeup of the main needle, done with my algorithm as I posted it above: 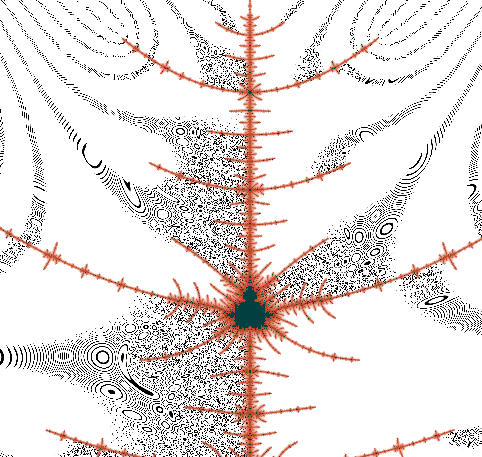 The moire patterns are nice and psychedelic, but obviously the angle measurement has way too much error. So then I tried the modifications Claude gave above. One really cool thing I realized is that the step size did not need to be clipped at all. Now I just use where dist is the distance given by distance estimation and step is a variable greater than 0 and less than or equal to 1. I also found that the binary method is highly dependant on a very very huge escape radius (more on this below), so I raised this as high as I could. With these changes I got this: 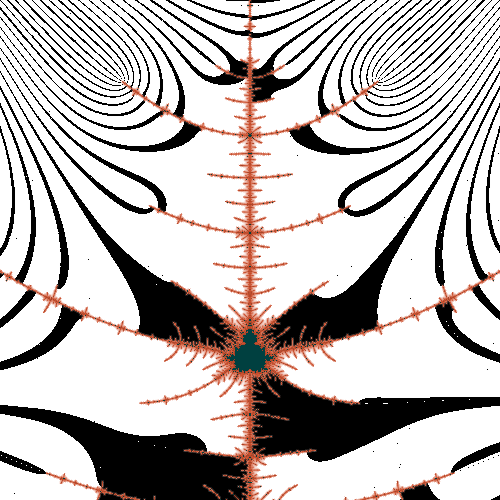 What a difference! There is still some errors creeping in, off the tip of each branch (look for black pixels in white regions and vice-versa). I minimized the errors by taking the variable step down to 0.05. Just for shits and giggles, I tried atan2 again, and to my amazement, I got this: 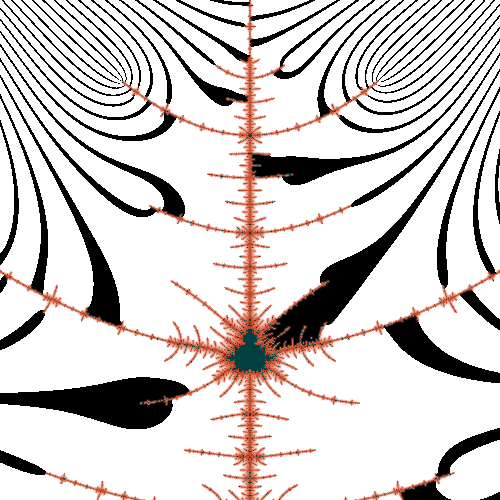 Even smoother with no visible errors! And I got this result using a step size of 0.5 which was much faster. So the big thing I missed above and that I got from Claude was making sure the escape radius is big enough, and making sure that I actually get all the way there before measuring the angle (His new calculation of 'm' and using 'm>2' as the condition to stop looping). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
billtavis
|
 |
« Reply #22 on: March 04, 2015, 07:47:54 PM » |
|
The binary method of measuring the angle causes steps in the gradient, which only smooth out when the escape radius equals infinity. I am guessing that the "horizontal positioning" mentioned by Claude above would help alleviate this. To show what I mean, here is the binary external angle using an escape radius of 3.40282e+38  Seeing this, I raised the escape radius (defined as the variable "huge" in the getGradient function) to the highest value I felt I could, which was 4.49423e+307 and got really close to a smooth gradient. However, the contours reveal that it's still not quite there:  For comparison, here is the atan2 angles, also using the largest escape radius possible. There is no visible break in smoothness, even in the contours: 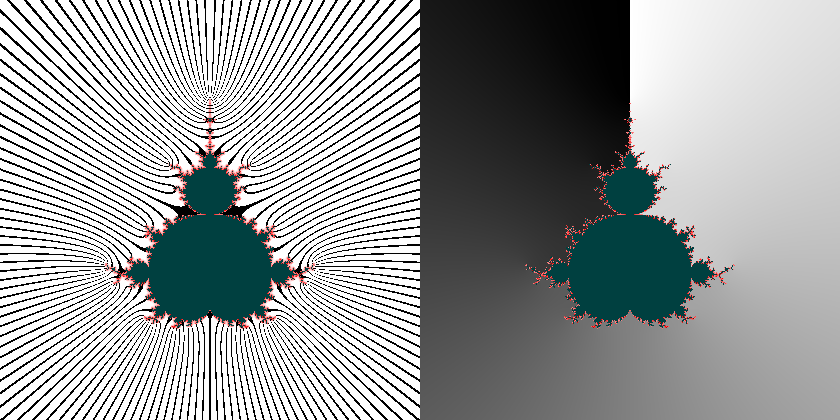 |
|
|
|
|
 Logged
Logged
|
|
|
|
claude
Fractal Bachius

Posts: 563

|
 |
« Reply #23 on: March 04, 2015, 10:11:09 PM » |
|
One really cool thing I realized is that the step size did not need to be clipped at all. Now I just use where dist is the distance given by distance estimation and step is a variable greater than 0 and less than or equal to 1. This is risky, you absolutely mustn't skip more than one dwell band at once, or you'll lose bits and get a corrupted result. The Newton method ray tracing works robustly by taking a fixed number of steps within each dwell band. I am guessing that the "horizontal positioning" mentioned by Claude above would help alleviate this.
Yep, should give you an extra 64 bits (with long double), which should get rid of any steppy appearance. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
billtavis
|
 |
« Reply #24 on: March 05, 2015, 12:17:26 AM » |
|
This is risky, you absolutely mustn't skip more than one dwell band at once, or you'll lose bits and get a corrupted result.
That's what I thought at first too, but I checked and using a step size of 0.5*dist was small enough to never miss a dwell band in the examples I tried, and there was no difference in the output compared to the clipped step length. And this way the step size is large enough to get to the edge of the very large escape radius in a reasonable amount of time. I think it works because the distance estimation seems to be related in some way to the width of the current dwell band. Although, there is probably a more direct way to measure the width of the dwell band? I'm still trying to wrap my head around Newton's method, it semms that's probably a more accurate way to walk out from the set. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Adam Majewski
|
 |
« Reply #25 on: June 24, 2017, 11:01:14 AM » |
|
; Thanks to Chris Hayton for showing me how to fix the "off-by-one" problems.
What means "off-by-one" problems" ? |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Adam Majewski
|
 |
« Reply #26 on: June 24, 2017, 12:22:50 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Adam Majewski
|
 |
« Reply #27 on: November 18, 2017, 10:12:56 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|


















