The concept of "infinity" is counter-intuitive in many ways. In particular, "infinity" is not a number that you can simply use in computation. For example, take a subset of all integers, say, all numbers from zero to one thousand. Half the numbers in that subset are even, and the other half are odd numbers.
The split between even and odd numbers remains the same, even for larger subsets, say, all numbers from zero to one million. In fact, the subsets may be arbitrarily large (ignoring the case when there is one more number of one kind than the other kind). And in all these subsets, the number of even integers is smaller than the size of the whole subset.
This changes drastically when you look at the whole set of all integers (i.e. no upper limit). Then there are infinitely many numbers in the set, with half of them being even, and the other half being odd.
But there are infinitely many even numbers! This can be seen with the mapping
f(x) := x -> 2*x
which establishes a one-to-one correspondence between all integers and the even integers.
The even numbers are now a subset of the positive integers, but that subset is as large as the whole set, despite the lack of odd numbers.
Or, in simpler terms: when going to infinity, things might no longer add up. :-) To come back to your original question: a set being infinitely large does not imply that it contains everything. Half of infinity is still infinity.
You're working with Cardinal numbers here, one of several types of infinity. Ordinal numbers behave like a perfectly respectable infinity in many ways, and it's algebra is well defined. One of the weird things is that
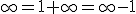
, but non of these are equal to
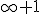
. Still, in most respects it makes sense.
I think you
would be able to find all shapes - especially if you're just sticking to black & white, because the cardinality of black and white raster images is much less than the cardinality of points in the complex plane. I think the Black and White Mandelbrot hypothesis (BWMH?) wouldn't even need to require any trickiness with changing the iteration, since any Minibrot will stay solid no matter what the iteration count, so if the minibrots were arranged just right we could get them to stay solid under the centers of the pixels.
I would state the BWMH as follows:
Let A and B be two finite positive integers, and let R be a finite set of points with positive, finite integer coordinates, such that each point P in R has an x-coordinate less than or equal to A and a y-coordinate less than or equal to B. Then for each A, B, and R there exist somecomplex Z and some real S such that for any two positive integers U <= A and V <= B, the number Z+(S*U/A)+i*(S*V/B) is in the Mandelbrot set if and only if the point (U,V) is in R.
How hard do you think it would be to get this instated as a new Millennium problem? Maybe we'd have to wait 1,000 years..


















