|
jehovajah
|
 |
« Reply #315 on: December 17, 2010, 08:58:11 AM » |
|
When facing shunaya one faces on the inside a mirror that suddenly shatters one into the myriad of monads that one is.
En. Wahed. Eka. Eureka!
'h¶h echad
Halleluyah!
Shunaya.
|
|
|
|
« Last Edit: December 17, 2010, 09:41:46 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #316 on: December 17, 2010, 09:59:56 AM » |
|
"I swear," said the sphere
"That my space is round!
But though i look
In every nook
This truth cannot be found!"
"I see your problem", said the cube
"And it, i think, is due
Perhaps an artefact, i say
Of a certain point of view!
Should you propose
To decompose
I think you will find its true."
Wear your cone!
You silly sphere,
Just like a dunce's hat.
To think that You could find what's round, like squareness
Just like that?
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #317 on: December 17, 2010, 12:53:01 PM » |
|
The roots of unity in the plane sum ro zero, thwerfore the roots of unity are yoked as one would expect in interesting ways that create equilibria both static and dynamic. |
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #318 on: December 18, 2010, 07:40:10 AM » |
|
One learns from meditating on the odd couple shunaya and monad the structure of my model of the set notFS which I have called FS
And we propose it not as fact but as some concept more fundamental than that
That shunaya emits the roots of unit measure but not as some have taught. The rectilinear and the round cannot be found in shunaya except as members of a dynamic trochoidal class of rotating and rotational symmetries.
The spaciometric version of the roots of unity I will research by and by, but this we know
The yoke of roots of unity are their dynamic rotational symmetry, so that we might say the fluctuating void has rhythm, and swirling in it are rotations of a root of unity. But the roots appear and disappear through the resonance of their yoke, or rather stand as entities of a standing rotational wave.
Therefore the unity of our choice comes with it's own resonance and scalar aggregational rules, it's own combinatorial structure and it's permitted permutability. And it's ceaseless rotational frequency.
The rotation is thus quantised but as we know there is no basis to unity, thus we quantize it by our own sensors that measure, by our own tools that we use to measure.
In this way we feedback loop to ourselves and our unit limitations. The fluctuations of the void appear from our iterative convolutions in processing our signal response to shunaya. The roots of unity inform us that this fluctuation is rotational and trochoidal, combining radial and rotational, indeed defining radial and rotational.
Therefore we imagine the motions of bodies in space, and space itself to arise from these rotational symmetries, like traffic jams and synchronous swimmers, to appear from the relative synchronicity of yoked roots of unity, and to move in coordinated fashion as if a wave, switching on what comes before and switching off what falls behind: a kind of animation through pixel manipulation or rather spacel or voxel manipulation.
And so our prime elemental substance lies in the relative rotational motion of regions of space even below the Planck length, these relativities being perceptible to us through our iterative and convoluted perception processing as attributes to space.
All motion and all stasis relies on these fundamental rotational symmetries which are the roots of unity dynamically manifesting to our sensors in a vast computational flux.
"This", as the saying goes.." this is how we roll!"
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #319 on: December 18, 2010, 11:53:31 AM » |
|
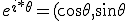) These are the roots of unity in the plane, but no longer the Cartesian plane, and yet still the Cartesian measure. There is no plane, but a space and a tool to measure it with, the Cartesian measure, the Bombelli vector, the Pythagorean unit square diagonally split. With such a tool we can set up our unit with which to measure a space that is flat and surface like. And our units are orthogonal lengths 1,1; √2 a new surd unit at pi/4; a triangle area unit = half a square unit. These are the units on our measure, and in addition we can do neusis with our measure, so everything is relative. Relative to our measure and contrariwise relative to the form we are measuring, and in addition relative to we who measure. This is the state of affairs as described relative to an observer outside of we who measure, with a measuring tool, a form parametric to us that we have dimensioned from shunaya, a tool of units to be employed iteratively in some grand fractalian scheme of scalars. And so to notation to record and to display, to calculate and to verify. These four necessary things succinctly put in a form that reveals and does not mystify...how is it to be done? What praxis shall we use? What mathesis? In the end we draw upon Descartes and bend him to our needs, in hopes that all familiar with him may follow our line of playful thought. So now we are nearly ready. On my measuring tool I have no measure for rotation, but I will add one and call it radian and give it a unit of direction called i and a parameter of rotation from that direction called 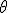 and now we are done. |
|
|
|
« Last Edit: December 18, 2010, 02:15:27 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #320 on: December 18, 2010, 01:31:59 PM » |
|
hello jehovaja, really the positive and negative signs are simply arithmetic operators, or if not they dont work with numbers, my proposition, like you said it, it s a operator generalize ¨of a way¨ the concept of signs with the help of mod operator, where, the 2 signs is a particular case (mod =2), giving de option of to work with numbers or signs depending when it will be more easy to use.
I think that using numbers at least in 3d, for obtain in a simple way some kind of 3d fractal, giving 2 options:
the last that i propose, it was to use a 4-signed arithmetic that is represented by a tetrahedral tilling in 3d ( in mod 4), and it is of the form ..i]a + [j]b + [k]c = M, 3 coordenates because of it is 3d space. and later to work it to generate fractals.
the first that i propose, it was use a 3-signed arithmetic, that is representated by a triangular tilling in 2d, of a form ..i]a + [j]b = S ( that result to be a isomorphism if complex plane), and later to extend it to obtain a of their posible analog complex( but for 3 signs , in six real dimensions ) and later to work it with this algebra to generate fractals ( iterating)
some other questions?
regards
Rereading Kujonai i realise that he proposed a tetrahedral tiling, not just a triangular one. I think this has been done in the tetrahedral folding of the mandelbrot thread. In any case i reread Kujonai in the light of yoked decompositions of Shunaya. |
|
|
|
« Last Edit: December 18, 2010, 01:38:57 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #321 on: December 18, 2010, 06:31:42 PM » |
|
Why i not y? Not why? but y. Way aye, mon, Aye! I eye i Sign, sigh! O Shunaya? Hi! more word originAt Jeff Miller's web site on the first use of math symbols I found the following discussion on the origin of the symbol "i" for the square root of negative one: i for the imaginary unit was first used by Leonhard Euler (1707-1783) in a memoir presented in 1777 but not published until 1794 in his "Institutes of the integral calculus." On May 5, 1777, Euler addressed to the 'Academiae' the paper To The 'Academy' the paper "On Angular differentials by a formula which nevertheless mostly results in purely irrational logarithms, and integrates the circular arcs pertaining thereto," which was published posthumously in his "Institutionum calculi integralis," second ed., vol. 4, pp. 183-194, Impensis Academiae Imperialis Scientiarum, Petropoli, 1794. "For me at least, there is yet another way, not obvious to guarantee that this is [it...the correct way], except by proceeding through the imaginary [quantity] , the notational form which I will designate as i hereafter, so that it may be ii = -1 and thus 1 / i =-i. " According to Cajori, the next appearance of i in print is by Gauss in 1801 in the Disquisitiones Arithmeticae. Carl Boyer believes that Gauss' adoption of i made it the standard. By 1821, when Cauchy published Cours d'Analyse, the use of i was rather standard, and Cauchy defines i as "as if was a real quantity whose square is equal to -1." Throughout his Introductio, Euler consistently writes ," denoting by i the infinitely large number of" . Nonetheless, there are a very few occasions where Euler chose i with a different meaning. Thus, chapter XXI (volume 2) of Euler's Introductio contains the first appearance of i as quantitas imaginaria: For when negative numbers are logarithmed, results are imaginary ....... log (-n) will be the quantity imaginary, which is equal to i. The citation above is from "Introductio in analysin infinitorum," Lausannae, Apud Marcum-Michaelem Bousquet & socios, M.DCC.XLVIII (1748). Please note that, in this fascinating passage about logarithms, Euler does not introduce the symbol i such that i^2 = -1. [This entry was contributed by Julio Gonz�lez Cabill�n.] And translated using google translate to help. Here we have the terms number and quantity used differently and i think after the greek. Quantity is magnitude of a geometrical form and number is a scalar of unity. To the greeks Arithmoi were dynamic geometrical forms that scaled and transformed and moved and spread and covered as units. Thus by plethora the units measured as arithmoi, scalars. The idea of number in other cultures was less dynamic, more staid,and scalars were looked on as and for results, Quantity was the same as magnitude, but not as dynamic as greek magnitude, they did not multiply as greek magnitudes do by motion in orthogonal directions by certain lengths. it was more of a rote learning of number bonds. Cuisenaire rods illustrate greek arithmoi. So negative scalars in logarithms Euler found could be treated as quantities, arithmoi.but only as imaginary ones following rules, and related to log of trig functions. Euler did not need Cartesian coordinates because he had trig ratios and triangles as his measure, and by relating to De Moivre and a unit circle he was able to tie all 3 together in a way that he says is not obvious, or guaranteed to be correct.He used differentials of De Moivre theorem to obtain infinite Taylor expansions Cotes had done something similar through studying the log of trig functions nearly a half a century earlier. Euler treated i tentatively as a unit quantity and therefore applied scalar math to it under the given rules of Bombelli, but as he says in his own notational form, with an innovation of division. By cauchy it was treated as a real quantity, and by Wessel, Argand and De Moivre it was given a richer and geometric interpretation. Gauss popularized it , and surveyors and scientists latched onto the geometric cartesian form, The cartesian measure was recognised as a model for whatever measurement tools were required, thus a measurement tool for the adjugate form was made by Wessel and Wallis and Argand. in which y was replaced by i but associated with y This tangled mess no one seemed able to satisfactorily sort out, and so piecemeal ad hoc rules grew up into the field as it stands today.  is a real quantity obtained by multiplying a quantity by a quantity, a magnitude by a magnitude but under a set of algorithmic rules. However mathematicians have never stopped teaching students that they are imaginary and complex and they are numbers. It is time to stop. They are not imaginary, and they are not numbers, but i is complex. They are magnitudes and they are units of measurement and they exist in spaciometry as real dynamic aggregations. |
|
|
|
« Last Edit: February 26, 2011, 10:37:36 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #322 on: December 19, 2010, 02:01:21 PM » |
|
When one has looked at the struggle of scientists and artists over the ages to measure shunaya it is a blessed release to see all their work come to fruition in some elegant and useful form. It is a thrill to look back over the tortured mutterings of feverish minds and gay abandon of playful minds, to look a chancres and dancers, and singers and scientists, at astrologers and philosophers, at artisans and housewives at those in plenty and those in penury mendicant and monastic, egregious and generous,in short all and any human engaged in human survival, and see that they all have contributed to the formulation of the notion of the roots of unity as a measuring tool. Thus it comes to this.  is rate of rotation quantity x radian arc length quantity is rate of rotation quantity x radian arc length quantityAnd all are unit and scalars of units and yoked decompositions of shunaya into roots of unity based on the unit sphere, the dynamic unit sphere,moving relative to any other spatial form. We need one element for this tool and that is a equilibrium reference from which we can construct all other equilibrium references of relative motion. This I have called a pole as in a pole or a pole star or an pole of orientation. This is a particular radial of equilibrium in the measure or in the form being relatively measured. The rate of rotation quantity is the root of unity quantity and governs the rotational symmetries of the dynamic sphere; in regards of unit: is to measure dynamic equilibrium rotational states. As with all unities it is a set of nested yoked unities, but scalar ratios do not apply, these are roots of unity and so by definition are not scalable. They can however carry a radial scalar that scales only radially, thus providing axial extensions and axial motion and taking orientation from the root of unity. They also carry a special scalar of sorts called a radian, and this serves to transform one root of unity into another. The radian scalar is motion scalar dividing the rate of motion into smaller unities that relate by rotational symmetry fractal scales to the standard rotational magnitude. De Moivre formula gives us the roots of unity in terms of i because all roots we may choose can ve written in terms of each other, because they are roots of unity. So defining √-1 as +And- 1 and denoting it by i and laying out clear rules for it's usage we come to the quintessential algebra of spaciometry, to the realm of Wessel and Hamilton, the realm of quaternion algebras.. Many have gone on beyond this, but as pioneers not knowing where or how they would be going, not knowing that they were dissolving into the mists of shunaya. |
|
|
|
« Last Edit: January 12, 2011, 01:40:21 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #323 on: December 19, 2010, 02:58:00 PM » |
|
In the light of spaciometry being the ground of algebra, I look at the theory of operators in algebra.
Really an operator has to be an activity that transforms.
Now the Greeks first created or distinguished unities. Is this an activity that transforms? Here we have to acknowledge the impact of the measurer the uncertainty principle. The creator of the unity the measuring tool defines the magnitudes, dynamic and in equilibrium, that can be measured
Having created the unit we use it or observe it in dynamic action. Is this an activity that transforms?
Again the observer may have transformation that is internal due to an internal act of imagination, or an object may be physically transformed by motions of measuring, applying the unit directly to the form. Or I may even be observed that the form transforms by shattering or dissolution into the unit forms in and of itself. The form may be dynamic alive and active transforming itself by units motions.
Our response to this plethora or aggregation and dis aggregation is to measure, count or evaluate in some way as precisely as we need. We may just compare, we may enumerate units and compare, we may measure and construct units and compare, our response is varied and commensurate to our need.
Thus to abstract to notation of -/+* is to just begin, just to note an observed activity that is transforming. And these notes must be qualified and explained fully in the form of an algorithm based on a set of rules and definitions to wit an algebra.
None of these notations therefore have meaning beyond the meaning given in the algebra. And because of this by design or default algebraists can make their notations confusing and false indicators or clear and customary sign posts. They can invent new notation with the risk of not engaging the usual suspects or twist usual notation to a different purpose, thus deceiving while apparently informing!
Our notation and customary signs and operators have evolved over time to have a flexible and connective meaning that communicates, but also confines and obscures.
The differential calculii and integral calculii are proportions bent to another purpose and so obscured by notation that it strikes fear into the hearts of those who geometrically proportion everyday of their lives!
So our spaciometric activities and observations give rise to our algebras within which we define our algorithmic operations of measuring, and prior to this we transform our minds by distinguishing which unities we will use to measure and how they are related and yoked together in relative motion.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #324 on: December 20, 2010, 11:01:42 AM » |
|
The radian arc measure is a mod(2 pi) arithmetic but we can utilise other arc measure in a related way but of course not based on the unit circle. Thus a transformation exists through similar circles to any arc measure we require, based on mod arithmetics.
As simple as it is we have confused ourselves by using the notation with a multiple meaning. So y stands for a direction a value in that direction and a variable value in that direction! Thus 3 y we know by teaching is a scaled value in the direction of y with the variable value of y being scaled.
3i however is different, and the difference is the additional rules we attach to i . These different rules relate to i being + and- in sign but in reality to i being a 4 th root of unity while other values are a 2 th toot of unity. We are not dealing with the same units, so as we know from basic algebra we do not add apples and pears.
We stick by this rule throughout all or measuring, so we do not add metres and centimetres or pounds and pence or even whole numbers and decimal fractions. We always only aggregate like units and we note next to them other units that we aggregate the result is a string of units across the page. The clever thing the Indians did was to make a pattern of these different units so that using mod arithmetic we could move to the next unit.
It is this pattern that shapes our world and our perception of it, for we see wheels within wheels and structures within structures related by dynamic iteration and geometric convolutions. We see the structure of our fractal universe and we know that it is an illusion, a playful pattern of our choosing. We have other aggregate systems, and we can create yet others.
Choose your own and enjoy the ride!
|
|
|
|
« Last Edit: December 20, 2010, 11:19:24 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #325 on: December 20, 2010, 10:39:19 PM » |
|
Of yoked roots of unity and prime magnitudes.
Of yoked roots of unity and determinants.
Of understanding measuring and relations and why notation describes active relating.
Of logarithms base 0, base 1 base π and base e.
Of the relation of mod() and log.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #326 on: December 21, 2010, 08:47:02 AM » |
|
prosthapahaeresis inspired calculators of all sorts, particularly astronomers,but more particularly John Napier, Napier was fond of playing and calculating,and very fond of trigonometry, spherical trigonometry to be precise through which he learned or rediscovered trig identities and the rules of sign. No wonder it appears to modern mathematicians that he was looking at imaginary quantities! Among other things the notion of a ratio being viewed and dealt with as a "number" is introduced through spherical trigonometry. " Al-Jayyani (989-1079), an Arabic mathematician in Islamic Iberian Peninsula, wrote what some consider the first treatise on spherical trigonometry, circa 1060, entitled The book of unknown arcs of a sphere,[6] in which spherical trigonometry was brought into its modern form. Al-Jayyani's book "contains formulae for right-angle triangles, the general law of sines and the solution of a spherical triangle by means of the polar triangle". This treatise later had a "strong influence on European mathematics", and his "definition of ratios as numbers" and "method of solving a spherical triangle when all sides are unknown" are likely to have influenced Regiomontanus..... "Every aspect of complex numbers and sign rules are found in spherical trigoonometry. We also find Napiers interest in calculation expressed by Napier's pentagon ".... To solve a geometric problem on the sphere, one dissects the relevant figure into right spherical triangles (i.e.: one of the triangle's corner angles is 90°) because one can then use Napier's pentagon: Napier's Circle shows the relations of parts of a right spherical triangle Napier's pentagon (also known as Napier's circle) is a mnemonic aid that helps to find all relations between the angles in a right spherical triangle.Write the six angles of the triangle (three vertex angles, three arc angles) in the form of a circle, sticking to the order as they appear in the triangle (i.e.: start with a corner angle, write the arc angle of an attached side next to it, proceed with the next corner angle, etc. and close the circle). Then cross out the 90° corner angle and replace the arc angles non-adjacent to it by their complement to 90° (i.e. replace, say, B by 90° − B). The five numbers that you now have on your paper form Napier's Pentagon (or Napier's Circle). For any choice of three angles, one (the middle angle) will be either adjacent to or opposite the other two angles. Then Napier's Rules hold that the sine of the middle angle is equal to: the product of the tangents of the adjacent angles the product of the cosines of the opposite angles The mnemonic for remembering the trigonometric function to use is that the first vowel of the adjective describing each angle (e.g., i for middle) is the first vowel of the name of the function. As an example, starting with the angle , we can obtain the formula: Using the identities for complementary angles, this becomes: cos(B) = tan(a)cot(c) = cos(b)sin(A). See also the Haversine formula, which relates the lengths of sides and angles in spherical triangles in a numerically stable form for navigation...... "Napier found inspiration for calculation in trigonometry and using prosthaphaeresis. Because he was interested in astronomical calculations he wanted to work out the ratios for a very large hypotenuse right angled triangle giving him very accurate values for distances calculated thereby. He based his idea on rates of motion, because the idea was dynamic, not static, he was trying to show how the sine varies dynamically with change of angle " John Napier, the Scottish mathematician, published his discovery of logarithms in 1614. His purpose was to assist in the multiplication of quantities that were then called sines. The whole sine was the value of the side of a right angled triangle with a large hypotenuse, say 10^7 units long. His definition was given in terms of relative rates. The logarithm, therefore, of any sine is a number very neerely expressing the line which increased equally in the meene time whiles the line of the whole sine decreased proportionally into that sine, both motions being equal timed and the beginning equally shift. In modern terminology, L is the logarithm and X the sine. (In modern notation X would be r sin .) "We therefore have a clear and expected link between trigonometry and napierian logarithms which Cotes noted as 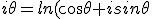) Changing the angle changes the sin but of course for a constant hypotenuse of 10^7 this changes the cos and the changes are proportional, but particularly identified by the sin. by inventing radianss Cotes was able to notate these relations succinctly and elegantly. In Cotes form the i actually acta as an identifier signifying which variables are related and the + acts as an aggregate relation indicating a co-relationship between these variables and cos. In Cotes time despite Bombelli the use of √-1 was fraught with misapprehension, Euler often made mistakes using it, so for Cotes to perceive this relation before Euler is due to a different mentality, a mentality based on trigonometry not infinite series. In that mentality √-1 has the meaning of the sign value of sin as its angle rotated through 2π radians. Thus as we know Trigonometry is at the heart of all methods of calculation especially roots of unity, logarithms and so called "imaginary" quantities. It is these roots of unity and their absolute link to logarithms of all sorts that i think Muses envisioned as a new order of calculus. Muses words. and his numbers
|
|
|
|
« Last Edit: January 12, 2011, 01:45:38 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #327 on: December 21, 2010, 03:08:13 PM » |
|
The perspicacity of opacity Is a property that's rare But you'll find it When you look for it Hanging in the air. The logarithm, therefore, of any sine is a number very neerely expressing the line which increased equally in the meene time whiles the line of the whole sine decreased proportionally into that sine, both motions being equal timed and the beginning equally shift. Thus a constant increase is linked to a proportional decrease, equal additions linked to proportional divisions. And what are proportional divisions? Well proportional in this case means according to a proportion. So which proportion? the beginning equally shift. means that the line bit divided off the sine is equal to the constant line bit added to the log. Thus if the sine is a the line bit added is b then the portions are a-b and a. The proportion is a-b:a. The proportion we use is: divide into a units an take out a-b units. When using proportions use a physical rod, it makes it real easy. Now proportional division is dividing the rod iteratively in this proportion at every iteration. This type of iteration is convoluted, each iteration requires a complex activity of self referencing, but a rod in the hand is better than two algebraic variables in the brain! So the pattern works out an arithmetic compared with a geometric series: b a-b ={a*(a-b)/a} 2b ((a-b)/a)^1*(a-b) 3b ((a-b)/a)^2*(a-b) 4b ((a-b)/a)^3*(a-b) 5b ((a-b)/a)^4*(a-b) .................... nb ((a-b)/a)^n-1*(a-b) So in this case the line bit scales up as the rod proportions down and the iteration counter records how many (a-b)/a are multiplied. This is called a power, an exponent, but Napier called it a ratio arithmoi(geometrical object). i can rewrite the nth logarithm relation nb ((a-b)/a)^n*a which gives (a-b)/a as the base of the logarithm Napier chose a= 10^7 and b=1 Napiers Logs are therefore not based on e. What they are however are a logarithm based on unity or as near as dammit, and they linked the product of the sines to an increasing logarithm. what that means is that the roots of unity are related to an infinite log scalar arithmetic in ways i have yet to explore, based on log base 1 Thinking about it more this particular log is log based sinπ/2, so this is not the logarithm of sines but the logarithms based sinπ/2. This leads nicely into the logarithms based cosπ/2 which of course are logarithms based 0 |
|
|
|
« Last Edit: January 12, 2011, 01:53:17 AM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #328 on: December 22, 2010, 09:45:14 AM » |
|
Of sines cosines and logarithms and spherical trigonometry in the measuring of shunaya by scientists of all ages. The secrets of the Yoked roots of unity and how Napier played in the dynamic space of shunaya. What shall we be riven with? What nails shall we drive into our souls? To pin us to the masts of ships To fix us to their poles? That commerce may continue thus Unabated by the storm? Nay! That sailing through the universe We may calculate it's form! Only a passionate scotsman in love with his god would think to waggle a huge Bombelli vector in space just to calculate the sine for the benefit of his honourable astronomer friends! And only an intense irishman would follow his lights and make a 3d Bombelli vector that reaches not only outer space but inner space! |
|
|
|
« Last Edit: December 22, 2010, 11:30:52 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
jehovajah
|
 |
« Reply #329 on: December 23, 2010, 05:59:28 AM » |
|
Warning, this post is very difficult to follow, and i wrote it?  I will try to improve it, but as a starting point keep in mind the metric and decimal systems!  The roots of unity are a special term for power relations between trig ratios in the unit circle. As such their link to unity is not as direct roots such that r^n =1 for a given r where r is a "number". It seems like we have to stretch our concept of number yet again to accomodate these ideas. In point of fact we should not stretch it but rather excoriate it! r has to represent an aggregate structure of differing but related unities, which means that one chooses several unities for measuring different scales, aggregates them into a structure, and then treats the aggregate structure as an entity. Then by applying the aggregation rules of that entity for measuring either motion in space or iterative increase or decrease,whether arithmetic or geometric in formulation, one arrives at the notion of scalars of 1, which ought to be the overarching unity, that is: the notion of unity that defines the structure of all unities. As seen above this is a logarithmic process and relates the aggregate entities to the "unity of the logarithm", that is the base of the logarithm. The product of the entities become related to the "zero sum" (of the logarithms of the entities),the modular "zero sum" of that specified base. So for example base2 has a modular zero sum of 2 because 2+2=0(mod(2)), etc. The "unity of the logarithm" is comparison of a complete or whole or unit clock cycle with unity, In the case of a p-adic logarithmic series each term in the series subsumes all the previous terms, and therefore acts as a whole for the serie thus far. The structure is a nested one, smaller bases/unites being nested within larger ones. Thus we have a formal relation between the bases in a logarithmic series and the notion of nested unities in a p-adic aggregation structure. What i mean is if i take the "roots of unity" as logarithms, using as the base the relation( De Moivre's relation, i think) then i should find that all the logs sum to 0 ( the usual mod(n) completion signal) giving the evaluation (from the definition: the base raised to the power 0 is 1) that the roots of unity are indeed logarithms of the base! This is very circular to write but this is how i saw it. The only way to write it clearer is to acknowledge this is a recursive or implicit definition defining the roots of unity as the logarithms of the base which sum to zero. Or to put it another way, as the roots of unity sum to zero they are precisely the logarithms we need to raise the base to , to efine those factors whose product together is 1
As a concrete illustration: if i use 1 meter and 1 decimeter and form the aggregate 1+(plus and minus)d where d simply is 1 decimeter, the (plus and minus) attribute controls when the decimeter can be added or subtracted from another decimeter during a multiplication of the entity. With the right scalar in front of the decimeter i can get it to disappear or scale up to a meter so as to make the meter disappear, during a set of multiplications. This kind of control of summation within aggregation by means of an attribute is what "complex" calculation is all about and is not obviously logarithmic,but is "modulo arithmetic" and gate controlled by the +and- scalar combination. This gate control is computer like,storage like and arithmetic logic unit like. It is only when the gate is opened allowing the decimeter value to combine with the meter value , leaving a remainder, that the logarithmic nature comes to the fore. If as Napier did we use really large units we can see then that the logarithmic action is in fact always acting and present. This connotes to using real valued logarithms as opposed to integer valued logs to capture what is happening. In short, whatever the unities aggregated the +and- attribute provides a signal gate control over the summation, providing the unities are nested, that is scaled ratios. We still cannot combine apples and pears! Logarithms in this case can be constructed to tabularise any multiplication of entities ( aggregations) within the scheme speeding up calculation and enhancing reliability. Logarithms as an analytical tool serve to systematise calculation and reveal proportional relationships of a geometrical nature. Roots of unity therefore are not numbers but algorithmic entities controlling calculation logarithmically, and in a way linked to modulo arithmetic of the underlying base. These algorithmic entities are fundamentally based on ratios of the right angled triangle and are "cobbled" together by sign rules and the +and- gate rule, the Bombelli operator. The operator +, or the notation + is therefore not a simple or even a binary operator but a "control relation" with certain complex relation rules applicable to given identified and identifiable situations. This complex activity therefore distinguishes + as an algorithm not just a "simple operator" if such a thing exists . Here is an illustration to meditate on. 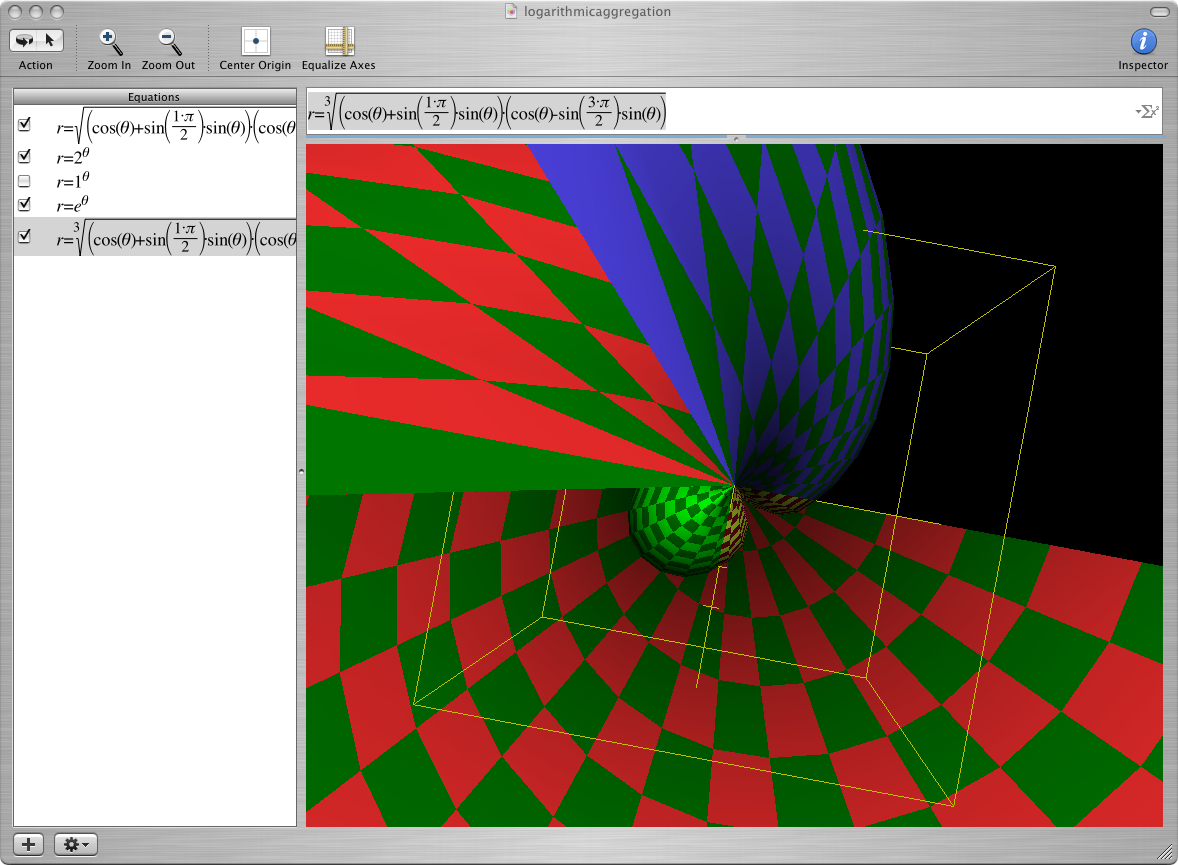
|
|
|
|
« Last Edit: February 26, 2011, 12:06:52 PM by jehovajah »
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|


















