@fractalrebel - mind sharing your expansion (code) for the lambda bulb formula? I'm trying to get it right, but something's really wrong with the pictures I'm generating!!
I tried adapting the 'standard' 3d mandelbulb code, but seems like I'm missing something.....
Thanks!
JC
All of my code object oriented Ultrafractal 5 code. I define a function for taking powers in spherical coordinates, and an other for multiplication. The target function is
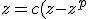)
where c is the 3D complex number for the Julia seed. Here is the power function. the vectors are 4D vectors. a is the input vector and b is the output vector. The vectors are a convenient target for the mapping to two complex numbers. Obviously the 4th dimension component is always zero (at least for bulb fractals).
static func Spower(bool altel, float power, Vector a, Vector b)
; Power function for s = x + iy + jz expressed in spherical coordinates
float r = sqrt(a.m_x^2 + a.m_y^2 + a.m_z^2)+1e-10
float phi = atan2(a.m_x + flip(a.m_y)) ; azimuth
float theta = 0
if altel
theta = asin(-a.m_z/r)
else
theta = asin(a.m_z/r)
endif
r = r^power
phi = power*phi
theta = power*theta
b.m_x = r*cos(theta)*cos(phi)
b.m_y = r*cos(theta)*sin(phi)
b.m_z = r*sin(theta)
b.m_w = 0
endfunc
Here is rhe multiplication function. a and b are the two input vectors and c is the output vector.
static func SMult(bool altel, Vector a, Vector b, Vector c)
float ra = sqrt(a.m_x^2 + a.m_y^2 + a.m_z^2)+1e-10
float phia = atan2(a.m_x + flip(a.m_y)) ; azimuth
float thetaa = 0
if altel
thetaa = asin(-a.m_z/ra)
else
thetaa = asin(a.m_z/ra)
endif
float rb = sqrt(b.m_x^2 + b.m_y^2 + b.m_z^2)+1e-10
float phib = atan2(b.m_x + flip(b.m_y)) ; azimuth
float thetab = 0
if altel
thetab = asin(-b.m_z/rb)
else
thetab = asin(b.m_z/rb)
endif
float r = ra*rb
float phi = phia + phib
float theta = thetaa + thetab
c.m_x = r*cos(theta)*cos(phi)
c.m_y = r*cos(theta)*sin(phi)
c.m_z = r*sin(theta)
c.m_w = 0
endfunc