|
David Makin
|
 |
« Reply #15 on: November 21, 2009, 12:20:28 PM » |
|
Can you share a snippet of code. ie going from the 3d point calculated on the surface up to the point the normals found?
Why does the "small amount" cause issues? I would assume that like when shooting more rays to get a normal, you step half the distance to the next pixel?
I have gotten the basic rendering working, but the excess of 5 rays per pixel is killing rendering time.
If you're using the method I suggested (which is basically the same as lyciums actually except that it's his method *combined* with the surface method) then the overhead for getting the points on adjacent rays should be negligible - if not then you're ray-tracing on the adjacent rays when you shouldn't be. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #16 on: November 21, 2009, 12:33:18 PM » |
|
*ahem* it's not the same method at all, consider the behaviour of the "multiple rays" approach on the object silhouette and at visibility boundaries...
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #17 on: November 21, 2009, 12:53:40 PM » |
|
*ahem* it's not the same method at all, consider the behaviour of the "multiple rays" approach on the object silhouette and at visibility boundaries...
Huh ? Remember I'm *not* ray tracing the adjacent rays, just using them to get my offset positions (using the position on the adjacent rays that's the same distance as the centre point from the viewpoint) - this is basically what you're doing except using different offsets. Also I should add that since my previous post where I said "I do do limited tracing if the adjacent point is 'inside'" I have stopped doing that because I realised that generally the calculated DE value is OK to use even if we reached max iterations (as long as we aren't *too* far 'inside') - this point was brought home by the recent renders of the "Mandeliers" (I tried rendering them and found I couldn't because as soon as max. iter was hit my algorithm said "solid found"). BTW - is it just me or are the Mandeliers just a figment of the distance estimator's imagination, as I recall for Mandelbrots of negative power everywhere should be "inside" ? |
|
|
|
« Last Edit: November 21, 2009, 12:59:13 PM by David Makin »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #18 on: November 21, 2009, 12:55:53 PM » |
|
Can you share a snippet of code. ie going from the 3d point calculated on the surface up to the point the normals found?
Why does the "small amount" cause issues? I would assume that like when shooting more rays to get a normal, you step half the distance to the next pixel?
I have gotten the basic rendering working, but the excess of 5 rays per pixel is killing rendering time.
If you're using the method I suggested (which is basically the same as lyciums actually except that it's his method *combined* with the surface method) then the overhead for getting the points on adjacent rays should be negligible - if not then you're ray-tracing on the adjacent rays when you shouldn't be. I did some timings with and without lighting and got 1:54 and 1:49 with and 1:54 and 1:48 without. (for "with" I mean without shadow-tracing). |
|
|
|
« Last Edit: November 21, 2009, 01:02:14 PM by David Makin »
|
 Logged
Logged
|
|
|
|
|
JosLeys
|
 |
« Reply #19 on: November 21, 2009, 01:37:04 PM » |
|
Sorry if it was not clear :
The blue triangle represents the surface.
P is a point on the ray. The potential function is the distance to the surface.(which is zero on the surface)
So we take two other points, a distance d away in the x and y directions, and mesure the distance there.
The differences in distances give the surface normal components..
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
subblue
|
 |
« Reply #20 on: November 21, 2009, 06:25:09 PM » |
|
I've been following the Mandelbulb discussion for a few weeks and have a GPU implementation working using Adobe Pixel Bender, but haven't yet managed to generate clean normals. I've been attempting to create a Jacobian matrix that Iq mentioned (further discussion in GPU gems), but without any success yet. Below are the differentials defined by Mathematica and the code used to calculate it. I thought I'd share it in case anyone else can shed some light.  So in principle using the code below the normal should be created with n = normalize(Jacobian(z) * z), where z is the intersection point: float3x3 Jacobian(float3 z)
{
float n = float(power);
float zm = dot(z, z);
float zm_n2 = pow(zm, n/2.0);
float zm_n3 = pow(zm, (n/2.0) - 1.0);
float x_y = dot(z.xy, z.xy);
float sxy = sqrt(x_y);
float atan_z = atan(sxy, z.z) * n;
float atan_x = atan(z.y, z.x) * n;
float sin_atan_z = sin(atan_z);
float sin_atan_x = sin(atan_x);
float cos_atan_z = cos(atan_z);
float cos_atan_x = cos(atan_x);
float z2 = z.z * z.z;
float xy = z.x * z.y;
float yz = z.y * z.z;
float xz = z.x * z.z;
float dx_x, dx_y, dx_z;
float dy_x, dy_y, dy_z;
float dz_x, dz_y, dz_z;
dx_x = zm_n3 * n * z.x * sin_atan_z * cos_atan_x;
dx_x += zm_n2 * (-xz/(sxy * zm)) * n * cos_atan_z * cos_atan_x;
dx_x += zm_n2 * sin_atan_z * -(z.y/x_y) * n * sin_atan_x;
dx_y = zm_n3 * n * z.y * sin_atan_z * cos_atan_x;
dx_y += zm_n2 * (-yz/(sxy * zm)) * n * cos_atan_z * cos_atan_x;
dx_y += zm_n2 * sin_atan_z * (z.x/x_y) * n * sin_atan_x;
dx_z = zm_n3 * n * z.z * sin_atan_z * cos_atan_x;
dx_z += zm_n2 * (sxy/zm) * n * cos_atan_z * cos_atan_x;
dy_x = zm_n3 * n * z.x * sin_atan_z * sin_atan_x;
dy_x += zm_n2 * (-xz/(sxy * zm)) * n * cos_atan_z * sin_atan_x;
dy_x += zm_n2 * sin_atan_z * (z.y/x_y) * n * cos_atan_x;
dy_y = zm_n3 * n * z.y * sin_atan_z * sin_atan_x;
dy_y += zm_n2 * (-yz/(sxy * zm)) * n * cos_atan_z * sin_atan_x;
dy_y += zm_n2 * sin_atan_z * (-z.x/x_y) * n * cos_atan_x;
dy_z = zm_n3 * n * z.z * sin_atan_z * sin_atan_x;
dy_z += zm_n2 * (sxy/zm) * n * cos_atan_z * sin_atan_x;
dz_x = zm_n3 * n * z.x * cos_atan_z;
dz_x += zm_n2 * (xz/(sxy * zm)) * n * sin_atan_z;
dz_y = zm_n3 * n * z.y * cos_atan_z;
dz_y += zm_n2 * (yz/(sxy * zm)) * n * sin_atan_z;
dz_z = zm_n3 * n * z.z * cos_atan_z;
dz_z += zm_n2 * (-sxy/zm) * n * sin_atan_z;
return float3x3(dx_x, dx_y, dx_z,
dy_x, dy_y, dy_z,
dz_x, dz_y, dz_z);
} I'd be interested to see Iq's approach to this  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #21 on: November 21, 2009, 06:43:02 PM » |
|
Maybe I'm missing something here ?
*But* isn't it true that you need the Jacobian for the actual equaton for the point found ?
In which case in order to get the correct Jacobian you have to iterate it in a similar way to getting the derivative ?
i.e. You can't simply use the Jacobian for the Mandelbulb z^b+c, you have to use the Jacobian for the equation of the nth iteration of the formula.
At least that's what I thought and is the reason I abandoned using the analytical method for getting the normal.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #22 on: November 21, 2009, 06:58:08 PM » |
|
just a note, you can use LaTeX inside posts ! like: 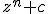 |
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
fractalrebel
|
 |
« Reply #23 on: November 21, 2009, 07:02:44 PM » |
|
Sorry if it was not clear :
The blue triangle represents the surface.
P is a point on the ray. The potential function is the distance to the surface.(which is zero on the surface)
So we take two other points, a distance d away in the x and y directions, and mesure the distance there.
The differences in distances give the surface normal components..
Hi Jos, Thats essentially the method I use, except I chose 4 neighboring points and determine the normals in pairs, and finally averge the normals to get a better approximation to the "true" normal. This adds very little overhead. Most of the calc time is for determining the fractal surface. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
fractalrebel
|
 |
« Reply #24 on: November 21, 2009, 07:04:58 PM » |
|
just a note, you can use LaTeX inside posts !
like:
<Quoted Image Removed>
Thanks! That will be vary useful. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #25 on: November 21, 2009, 09:40:03 PM » |
|
With DE I think it's quite simple to calculate normal vector because we can calculate some central differences or gradient of potential function. But what we can do when calculating of DE is impossible, for example for some strange non-linear fractal formulas? Now I know only one method. It is not so fast but gives very accurate and smooth normals (fractal details are also sharp). It is something like central difference but average for some area. for (double xx = -1.0; xx <= 1.0; xx += 0.2)
{
double xxx = a + xx * delta;
for (double yy = -1.0; yy <= 1.0; yy += 0.2)
{
double yyy = b + yy * delta;
for (double zz = -1.0; zz <= 1.0; zz += 0.2)
{
double zzz = c + zz * delta;
double op = 1.0 - ComputeIterations(xxx, yyy, zzz, N);
nX += op * xx;
nY += op * yy;
nZ += op * zz;
}
}
}
double normalizeFactor = sqrt(nX * nX + nY * nY + nZ * nZ);
if (normalizeFactor > 0.00001)
{
nX = nX / normalFactor;
nY = nY / normalFactor;
nZ = nZ / normalFactor;
}
Maybe someone knows any other universal algorithm. I tried to found something in Internet but without result. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #26 on: November 21, 2009, 10:04:58 PM » |
|
@lycium: Here's the difference in the DE angles found using essentially the same method I'm using in 3D and the analytical method on the good old complex 2D Mandy, just compare the 2 layers, granted it's not perfect but it is pretty close: Fractal2 {
::1/Eaahn292XWPyuNS6+uB8/hC57ucKlrlvQP4xLNMm2+OAn+xBogORqsK1W5ykL1pq5X/lLa
jSUSMWqbjuRfqUM+YEBpo4SwvY/lU4WaxP99f3DPcL/WRWysf3+Txze4b57u9ay6lzf41s8X
e9WyytzfoI9jsLXTi1SAXy2lf7aysfN9t8dP8np/d+x/PRR/Ys6/Of+Tz++vzUaD6Q65b5nO
mM7fq/pHUwf6cKkf7jko5zf4Q2tXPtL5w9ib5nTve97/uDpnPnf8FrsZHvldJ5Hm/4qfUV20
XOmE99f3+TXUlP1UiDpvnrLiGrzZXgXzg/O50+9PsPvI7Y6Bld9lbpH3leZ3j33fYmWGFoX+
IZ2/I7Y2lc43toZey5nLx+XKU6SysDH2/49iv+T/5f+7P/lvlfDe9fcJdXuCgvUc6cmHZe8t
nfxirVl6+wy/U/QvCrqxrmKK4C+SpGdVrRJRP6r4nf+Q6x7pFJHP59R7+Q9Evyd9W6lbJz/x
5eeUW2O9T8InqB4a2tkof7H229RZpXK+409b+rwDn2ll8P195UdB6+w0jvo6n6r+yKyeL10L
rneme4ravjXxudJ9419ZXKbthTHOc6opB/fdJ98/q8pzmSS328AKd1fHexPjSkzPf+SW6udR
JBW2rQqyzGFMwxBB8+7HBTjSR+RVzeIofS1fLY9WVYEKuF6w080ve1f/zXzKO30woeH05tP7
THoJqtoTNKT1QWzQgzk9CHRwxHsZEB3l/W2FV1ejMC2Bx4iTrB4QLmawvPyuiTs6hFRKmeIz
fI6x4VYlU119c+7Z4NwvmmXoHud9qVLWjtOfL9Io0Ys1ptNN5/603yug3Bpe7ngD6suySinU
M4UxpLqPu45dvfPPrY3vd9W+h0bnu8frBaWwQh61vuSW93EEtaAIGQo8B71meWlprmFxKUYc
9wpTqZM+rVvFjS4/99i80p7j5KkZiC/au69QVP0roE9uaqJZvf7+lMsV65TFpXQrp5vn8l7H
QJjZmO6pXrMwHV9If8hf28LzQhyuK3jFI9/8hyu3mO3nuMDlX7cx9XyPi1+1ahqnVnPzZ+An
RLusrS5qf1bGlKgxLgNIQ+toWKR3XINWJd8qaFzcGY6rpXzYokq2C93wMTywUBGQbXLqxAiI
BOpBirlm0gB1Vt6Py2d7jzZ8Q48p8j34Cx1czcfJiS1ntji3SS+dnUTpKg514XanRXpV/5vd
9UR+OyqgCA1S4LSo1N66h0iCtP0sGUieQ40R6uQgvPUX/8ciaEY4FVPmrPUveIqa/Z+uQ90m
VfS40OqvHqBg5ryqHbWfZrNYwOE+P9X3LKGbXGCH7Wf8j1nbahX1aiN4lIAgHVWr+fbAck9y
IIQVNpOOVDompXIiTtC+K/qBeGzswFSz/vBSh8CVeX7EqGdniC5D4X/86vWitY9XbwTo+rNA
Ka/VejjreMhhxLnJGKZwsdBuSuvsFQV6jZfzZ3UNewmOPqSMjB0OT03A9ceoV/n06L2DP1Sl
sD6tvcZWHSYjZVnRXMRsC9/O/MyuPq/pa5ehsnadkrcz/xtDCDuRujsKZAy3lhfm6VyFjVw9
F1bDf7u36e2mWFajN2gKjlw6AyNqfCwBlmucaksvohc8v0PD/VDqcWyfqE+LHU86vQ0r8+tT
2Rsx+Vi8bfGu5GUZ4mdAhsb2BFB6Wm9p0tMTiulZi0tMTuul7zfP79zYHpM79PDXcDqMcxOg
Q2F7gCTX8h0zlhBxs/4Q6LZP8zFFzwul2Vb7I2WK9kVql1ZPa/Hlrmw8oZkBlRTVHYadcrf1
obU2D0hxsc2fPyAv9P3ubvBv6++/a2+07F3qCgEavBMQtp9x/32Qbhvj2BWeLpcYc3ZVXjLp
qEteZMSkq58zvXvK7/5QxgAFY/ftrJ0OnVZ6w4iasgwa7HanU+cOoeJ78N0TOxBhyzJkHGve
6bnVuob3y4MWnyH93Zfof+9LXTmV+uarDDW97/nZf8L2CMTm65x3M1jMDI6DYlFU/jfl9wjD
UD7V/dLfncVhdrWufQ93XTWKEogdBz6/Yeyy4Nbjeaec0ChQP3ewZ7yefeyc514IlG/0ynWv
J+pVirxRC201Snjt68ytzfat46ccS8nhOvQpzb3uMax6PBdeRyiPDdeZVfj5LnLuOvMZ1ngK
vy8CY8qVrjkv78qkoPDdet1NPPe+ngOvOJ+zQn38ZOsxmkFfG68WrOvY5mtyP482kNrkXlfS
Pqx61LXGHLvK/Uyi4VI2+od/77XvZC7e07HqRUTYTMzOfnH+vSvkqWTamd2/zQh1lsdY3I3d
/7XukldEvYft4O2dNe/zW716xp+iSFKuLZ+3e/WmdSM7y2pdlX+TdAxNjE0c2N4GIMP4gWL4
gyO7K1qBzu6NOIqcbZavlyRZKjdC4W98Rioe+ZdEDcNrIDUNM/fvkb1T9hY8gph4h/U/cTzx
e0ov/Zj6ZCKB79VxgexHE0UoI9A6NVrtdeYfjy8bvbHTq4+18THJg3/zh8jIPnwWym+uakKa
Crq3XSPcIl4rwPqqbr8Erf1QVFvVoj34neiGCmxtsYsa7GaYoHEzCRU0SkQUfXqoe8id3fWb
PJ+HULrRvajSjmyDnmTlV930CSAXAb21XGAmr3wX3PiY2D4/wOe45TXuNjCksc/VIY+//2l0
znpcWiuwkbsF0btXFKnf2CQ2uSP2MiwcIN/4N1/L96Z9XJ+wOFnrERr3rR+iDJCvG1DfuBik
fIbFIS0eBzHomX0a22Y5AuTIOxE48iM0bEpH9Kqsl3Ov9PhW+oymerhLTTfUZbfZoNJUTUUZ
jvB1bS24HV26LGyXyMt/onAW9oI5Xuc6Cd53Xkfmu0XzSPUkd9K5+vMWsoLEOLa006UtyRML
asFm4X8YLhpsIyWiTaxkWp9soSj3g0KLdhs1kDMQWtMTWrw0tK4GNmewraliG8It2zeQWtG0
q9fh8qa7hc1aRrW5e71M/IT0bWTqB9qFmydNpdqlm1mWuyc7CUL+gnyTcZq9dBlLX1Op2y1s
aXuKPoJty1eYQZFsdAh8KZ7iD1V02BnmV2aHH6Jew1sMX7EcxvW3OA2smX7IORLpAG1V/6qM
HaC9F7qftrD7nrfoh5SmxuOkaicdwU/H2JyZ+F7X1FCblTxe1Ar/xS4fUA4t/T7c68t5zS4y
tTpoc15iAn6VhyQtRIAVvKUtdq8xbf7uDc3i7pw3zmfL4sS6XfCspGjCOI3sK8if3dR/Tqa6
u16yMTGPVV/9bX2p14pK7vJ8Mnjjn6QkZ943d1Zb7FYKQeqHBmUkXU5PNJPwK0En8hsMTlyD
yMO2gJxm1BKMJ6cOqBvgrnBmdPJ1TDDJVacL7d8vmVFZjvP2JXgfuD1wKwBXYRh+twxBGngL
n1FULTz6dfG+sPExn9hM+sPkynVFi/dPkMBuNjtgWgbzoLa8vNju4JztZ0FT/3mRCYevi76G
pBiQ/6WILT7TL04d3l6BXHXJtXdKpDJnpzrpARDkf510zZ7/POQ0LybshaM0kg4VtmQ4IEbQ
RZg1At/rVna7jUVreOO7O0q38gibMcZ9cdkPv6eAqXRvS3s3o/D8tdLXxM7XtBu2bPEtmrRb
IJvo4F2dQf1aOYpDPdmqz+Lpga+Sbsv8vhLc6zfWv8Cu4k+W2F9Bh/XVjgmWwExcDX7+Pztb
DO2LLTf82lDZsNzd3Pc4jE+9Rvc+VCT1sDM6LCJXDyukE2qyh8d6VIwEliTf7May+rPMvm/y
rnVqzaTPn1V/nNc1us3yKumsl74Jve6bHUj5bnPEbP/+i0XmT4kX9Nuyc9AL2pBsJi34cz5P
iyhzCAyxXmz+1VtLOSIXckcu4IJcxRS4ijSijZ/Wr2LHLkXOWOvcsEe5YJ8yKQiKP/MJ81LE
yXvQOf9CJ81LkwXvIZxiSrSCf9Sh81LlzXvUCf9SJ81KQW/4W70ZlwZvSIn9K5c2rkwZvSCn
9qkFP94C5c2rFyZvWOn9aJc2rlwZvOJe7j29VJWCn9Ghc2bkzZvRCn9GJc2bSW94a5+84Wh8
1blzXvF9RH5xXvVg1pp82bTieqcBWbFZgknEyf/kc+7nkwf/kM+7nSWs+xV2F0KyYJRzpeZD
8usm5VhO1m5s3TK1SbmLhr3oUC47V4s9R72/tQk+6RRi67jk13HlsUAffUdw+JRLgaFmrs24
iIZ6+HLaTQssNBxi0EELaTga5nLt24chGBahoNBLktJYB7N6T3EoVKhmAouNQTdHWj8JhGJa
potBLltNQvyQBaE0a1ch+0puVYZSc56VFasoVi2IsS2GhV4jyKfNCrqbEEYEcdrgm8WKjWb1
MQpg2u83MJrx/60xMkKkNGGd5nQDBaY3UfahotBUWnPdFCUD6ar87f2SP4lsT18tUhJ/4bZX
uZ9VoPoDXQgTHOf6KDYoGb+Vy3rF30SLRYG7UDtb+pFQGdhjPJZ0Fx64G2GuW0De4uAXHpwW
VlX4C7CerYD2Gh/yEgwuVSroB2GhEEDJYXUJG/v9s/qg91eC9Mi4XXkJFevdhgSs86iB5A3t
DMUjSXXYaFSu2prxCtWBhrd68ojEXX8aF2t2Pguk6XqKJNKufvRjTysf5+1bnO8g+Dp2Y4FN
R/6ioDHCbQs1Hq5Dd9Q12bSJTz3hAgt3xJDzCTh1MDCZGDp2jYXri1v2h9oIEM801pAzXaUw
ZECwBg+Ohoc4AqszP/ORiHOIw/fpR/wIwO+zB8T0oiYPYTiQi9gTFtEb1R+wVyQx259cjxco
7xRg2pSYYsYpIr4QqNpfnvP8sJu4wrHm0XcQV0RSkYcQQD8oy4gqjcKEaMCtPi+dSNUtP6zp
hF4Rxxhr/4J6YE6PZ6OOc9HPpHjQ/JT9xhr/oJAZEqPZaQOc1HPZIjQ/JTJyhr/4JGZE6/mP
/hfwTSyI0fyUlc46PaCTGh6Tm2kDX9NknMJsZRNWVq3nJvi0vO4zrIexUIeFxL2yxrIegXce
FxfdQmXR8DHDeFxPg05VEP4JKviMF+SzrITVfis8mPLeFJA8lgXRCoakiXRmsqknXRmsKFgX
RmsOYeuCf28Kyk1DrDeQYeFZSYZf8EyzrITiMDeFZSsZxrITiOHeFxL4u8KCxTLpVy9zO9iq
M8Hiczo6NKoKvM+npnPreC6kBWZ8PAYf33QSKol6Q+7QyXufAXu044LFZXVW6vnnVs7B9mWf
FfKeP9IYA5LmNU9h/QNXr0b5lcjMpMGP4OXg/K7b3Kh7XLrvf76t8Dp3ORLj0DcSWrNQU9AO
YU1VtqAsSk9aAraRyK9Q2FIQa3Vbhqq545j6mhjW8tHGXdlgfO81Yb+6VVzKNIsJQ5F/IRN4
iqbbSESpN1Jg8rBXPkWU8108ikof7HWxI3wDtPDQ7ZuyjbaajN/gjpLcylBGKBsmea4Qj9dB
tmUVcAFRr7fnfGQu95nKnmL6x73rGv/0x3wWdmThDQ+tVz5CiVoUAy3pHYDdipqUwY8+ka6f
CElyraglzaGdQh+5d7ADfKvqJZ2LqPrFsc+WbqI+MXY86zQ098+tTlD+j+QozfXvIa1btI7Y
rl5t0C0fkK/2nSjbLYZ046iC5GXXYE4FisPnXIyE5FiMZehITwXI09qf/M6Brr4GOh9ztglh
f2FFy+ZXYY6nPke+Q2tXPtrelp/cRB6VlWveDOpR7OrPzYL0i3PHUZ0g1FnWbCgl0z4mWs9B
Kr01O0i9KVvAYPKLZDrvhqOlpUmhOkwZ3HXyvvMFwSFHfDWPnt1D1Q4bKcJG9ehBbs44SMm9
chlU465CRVk6xDky4zzEaeWzjlzqVwkZQTsQzb4KyGW6SNIpPkZHQeBVFMjFvpqDahh3UoyM
C8mCeSBfXY6ckE5F8B15Ixb/YGtdBp14D0uw0ayxYXQaN+wrLMtmck1FkWjOo6CTpJHPdBp0
4Dluw0ayRRXQaN+AoLMtezn6QI4Dbuw0ayRMXQaN6glLMlmccyFkSbCROEb2VTcxhffcrzVk
Q3gxq8ahMDFYXy2hePoLzOkEkTf22AxMUu1tD0DVqSY6HRU253wKsoKxmV0P1gBroPqBmOxy
E98HZDkdibJ7xgSN4lqgtXMKZ1UuBqUF89iHJD8nL+giuSMwjaZquxXkdMKbQGRBQSBSUjwU
iXoKpJHWQ1AQN6fqAgRQ+UBBrY5pCEOhsTJ3OA0SaTgn8dvpL1fQPf3D8zNcgQZ8eQmUePIU
OvH8k07pdRHrhrbexR0cfO4Jt3zNlZCey798z95gnEfvMZo8uILXuP3gsO1n/hAN/R22f7Wo
9p0+HZ7AUOLRh6AEZ7BY71KX7UktLgtvqsdBis9BsnGmIQfJz0LgWSO0MkS+lLnuwAg9F5nZ
I+1s0DFZXvSvjMrb6jDGtulJ2WfmpwWocROE/8a9idYIve2BUF3dxP61+Y8KMyBtNY6JVLJU
enFanR4Zm2l6DY56ZsdPon4XdwscpS17YAvcKrD0lLZqeRm8zjsgT+g3u0J7w6im7YbVN1Lh
q8ADZlvYbhLn0DrrXwuqKrXgfKhFanS7pmBYdAhcCftFK1L4yGmDcRra1XWK+kJa1LFziGtk
5aL8qXXmNWZpmAXbhY9i0MIqXpGJ0oyFfdUnmL0qRduLzFa1TlI2s+6flWtaOvr0qfwV+FD4
psvTr+w38PLZUGRuUrDUJl3C1dS0XxOREbzI9Zj0/etabDzEBw9t7Uw9itOZFI9NbdyKUitF
ZU0lciHerAJucrhUPSd7Wnuuk/6tOddKw9bd6KRmZG53jJxNcd6KSiJO5FWBmKlHcJvb2BAN
195eaoZsD4TDOr9Gfa45sr5+RXN3M7K4MTQD5lD9W27AhkJaV6lvb8Wb3gJ25D+3BRSI8vDy
kR4fvbIXz7unld5jPJ/2Hy43+QI/2Hi53al93F/+K2GbBuvidgj/9VsDgycfF7Aq/7rIjEL/
otSE6g3GaZakaDHvr5Tf864Op9SU1d+3ZG//ryjd48XMZgeyZIemDU0AiyMPfVrLEOmyWwos
xak2b7wwI3yDV5dCPkJ9PXcjjbrKVUwmKp9gomUrK3O29fVCz3ej4n9rWt8tHiWz2uvmpPWh
YbCpc5q1sATHx2cVIdGUpdGkjtLTfM3qVhQa7G7hW6bZX0H9uBt/SBTaBXIzPezclSs7tOeq
huHg7yhM+tD7uf4wHJC0j9y5XJne7bwJ79z8tJ7CY4rMHy3RPx21ATxpvpMK+48a+LveuaXr
XX/f2wW/yeLr4K10wVrxYe903Oo+YgdKT8d/6U2E3kno7AOCk8EbPK4c+dVVDZJBKHfZO/3h
NpILR93Ry6vjExfHJi/OKJuMrYtSC/eso+9YZ97xi43jFxvrQJ6RWJ6PXH/CRd8Lk1xvQEH/
CRc8LSWs4RW5zcXH/SRd8Ll1xvUEH/SRc86kz4j8SA0ue+Vi65XJrnflIe+Vi45Xls4pH5lO
id98rF1zvWWP/aR88rFxzvOJe7j8y8nue+Ni653IrnfjIe+Ni453ksqMdzLjjfroO+ty643S
N7n7443KxiEVu+tJRlD3sWoR6fSUn/Ty68fSEn/TC58fKZR5XZXtWme+RzpehL8vWq5VRDmQ
LmauI+/o61ULRrgCtyx9XK0ncjiktVIS4WhIqZge3Wh6VaHLSzga1trsm5Ch+AcUsstDxC3O
ELT7QsstDqV7u0amzlaUpFy2OsQ42hF83HSd7Q9CxjkphQz7GW78JpGYapsNELFuhQvsTJaJ
qXZuE9g1NFLTK34ttSN00KZbJWJcLxK8hQm3Wi6VqPfhQvVoJglyIUnxMW3l/Wu+sx+rTHzo
w4/dOrdDj5VmSdYkqlA+ZHGNEsSfS6gG76pi8dVcO18tkxJ/4bZXuZjuVa5ikGUgTHOf6KHc
oezEqBwaINN82rFmYZNIody3usXAxoMpHe854ieQWFs02rkL30BE4mLNMhHd5lpSgMAUD6NB
EtNcMkMp/AdTG7qqqMtYxJP/0ALns6jjLoMCntBPD7E5TD00TbPtxgcS6pBEepknW4wKB80g
TTcIb850y5ONw1E5x2PFSMN70AYTsGbHxhWm1pdqFp6jQ2v+TV70olM7Xuf92pDay+tJF3Pj
Dk5NpLR7N8p1nxlA7qRwtUgFwZQxWQaYC4y79l+n4k8qnAaOD02NfsXHZjtDkZRoa4AqUJmR
1oozI4nDBepIf4QqtzPTlCiDDdiERMGwj/kQnIpE7D8SqJm0ek3HtSWK2gGe6pwDeWCL2OtF
DrFfSA3phVAt3cBD57KGtFHU1J+YA9xnNFGjoiYSkxhVT0oz4wwmJpGHWlQiajxo/RMTKtho
/RfStuMJ7YEWAeKPGjFQm4jRYB4p/YMWAZSQGhFgmKkxYAkJEZEGAeaRGjFQmckRYB4pIZMW
wm//wQR4pLZMWAZSTGhFgm6kxYAkJQZEGghGlpBOLCIrWB/MpmFPVCfqZxPoCRNL+BXOqZxH
+iTNLDUJkpmlBwjB1sMAi0pmFfAKK1sMZFIN1sMZFKzKg+somlQqAJomlQqHpomlprL5pmlp
rTBomlprEunSxnN1sMdFx7YMEmaWmGX+H2h8Uzy0QzgaWmGcWUzy0wzhaW8juL1sQ9wXalrA
Nz6oOhB2FtzPbTf5z15218jXz3l9TOJRvjmAj409b9fUhZ/hfYfeR2R1kOSmpzi67Svs7x7Q
xMdEQc5jkZ/am9E7zvpeDVNSWleZwqJ3qZTQIJztsKay2NRrVrov8X1ZqS7vHtOKOa7qVlPo
cPFsPb56VPFV+gFNSsatS/tH5f7684p6qsKgAULe97/Oj/yUQI9sWnTm9fkC/9LXOd/4uZ1l
VrS2EiZ5AoKv53/dHSPfW1eYFPzcrr/BVPvfUV20XMT5p07bKh6lKTwnYSEnZXgXzg/O50+9
tcpfp2lu/QtL9PV/WWxXvcq6AqUO+L30thPU1eGb+36k9uqpLZ9qVLWzv99LtbfLDyFt+8Ps
Tpo6Mc+lyellKnTn0O74beWxuf76t8Dp3OdxX5dnwinnW93NTDon8VZlmJLpePV1aUWlG1cz
p7kSytdh+1830vwd8WvC8vvXk3cLw7kJV1fz6nP+ShqTf3nd/aWFNU4XYDDMp772D183T+y9
D+kJ1UXaOdQNilyb/4D2a3r/eXu+tYoq86/5Dj3Cp05zF3VTaZAVWjYW356W1VqqOGvKKhw3
sXHqgT1a3CyA7f0IRlPqufi7O9PkYK7/5qhI7BhqrW0Yi3+1a/lYs+c1oo+jsdmVMGSBPfKX
tE/wKpdA+JKc1ASRxbHrY7OtL/tGWW3fhMvHV1/ZU0yfzGIbTAoqcqx6KSGtZ86h0iCtZkE9
b/wEGhJZrPRlCBbGa0CyO0FcaDR9BnANDdeJZiq8cwWR6udK8yVf2c8eK6yFWfqzlkbV384d
XmjacpDfslWS0/M/nUEn0w90ipcU8MuKAQZftEigui1KPdljJWKNC7rRCsqI+2vgehVVO77r
e+cvZUffC3Zud9Lw+Gik7Y23Gw72w+djJ80O3el3TGDZCJqZpOUS10eMiUX/78ze8unK3rlB
GgpMWPi6DnN8V8OXLAUzj28RzBfW8A13+iWZkdEvK0IXAtTtL7U9jdKcQd8TpZBNyFwrxpIs
AnCHiFke/2J7LdD8Ob+NamYjcTbiOldKN2pwB1IlRsRKDRjUGmGpMkWw+831c1l/3iqopSsm
XjcTbeOldKt1pwhYeHSPXuzCzM5puH+5iiZ+W2VdEs63T0Ols65aq0EfrDL20uiOlu1GPN2i
iGWqmtYfEJa4L2RjlUbmvpsNPUERayOCOVL7wSOc4dajD7ghyTsbGqgdDLTcyFjXwuBT5IyV
GskXnsgN7o40F1GijOR34oqergtb4AX0GPnzCHL0d4cEd4AOEFGDFLhhCSnwEMUxGKCADVe3
g7DXt2Pu9QVrR4dSDFtdoq3WBSHu6tfMyhqebF+b4q3+R2Gq6tJo1wVt9jHNUVbrQNDX92PK
yQVvtCQMc17GednbFWX4q3+RsFq6tJYswVt9jzKUVbrQoawcO/AfUoX+XsfU34L7x7ZdkdzZ
ieTD8ekrfyOck29+ZxwRj1E/CHyGA0NvD6EbGDW4RinjBlZiYzYA5COOLGQ+hjZiBEwN+HGW
rGJWGGQIbcJM2zbFgBDUmuBLwQFrzB/PQx6fI+DUQfHI/AF15w19UsO3j7B3oI6b9Fq99C5m
eRYHvCd7uKT7LeS55OZ7cvCFiJXVQ/Zu8RLd38Tu/CPUWIfoS3NXj7fy/NlneXjeIEu/6M2u
K+ELwuM+EFTXneZs7JrgI+uyIS+yIiOzIGezI8uzOJ/6B7J7mirHqYOJy6hKU/0Vt/SO9Uec
LJip+0SQ/TBqVBGZqQtKV7kEt/Chc2RuCRcWSugEe/YkzaqnQIm9UPZROLqOyTe2UdwJ8ZV1
RwxndVftFxss6Ic7oAdyiOyEv6U2pmAW3iPxEx6U8pnQWHBCZiZdExT0POkETMXNXgP0bDr9
fnSmGF8vJ2c1Q8frQCSadW5Zor9RAAQeY2+3ejdh7xDcM4+3/iQHQuJ+ZpO6sDCDMUdNNEF+
41OwSsLDrRy7igvh1bzfK4Qz3A9l0REmeljP0v9Oqhe8fXkp+xAXUw8lheWmnPTY7RdEJWh/
VjuyF8nQcFE33T6ILqPu4KL2v04KN+P74KPivB1NO7H+DSV550B7EVnmPRGpGNCG+WLYL8kn
JuTpD6U0bS6mUtiPwYFfgyK+IcroVipE/W90S4gMG3yHyu34KRo75jrUBuYz2JVS0tptkNUP
RryHW7ULBCvxtdSZsKjW2NZWOgcIME/JmyhLsb6n8wwfKtSEvmiTqlcCJxYMdzQkY0w6UAZr
s/4UiUljHXuadYC0kHHnqkVZrxaCtdS1vMdMGYxry3itT1iTJTVCVcogsovEtzYiTW225Fxp
bsan9Dnq0tyxhTVU3MZ4kqR78V4UF2NrEOVpry9g9S7gTWNOJXwJ7CXmCBD2kryRgXDvf8cU
dkbll/msTcrc53kltVG7LEbMCnNGh0GjQYjRIsRTWybV4mZMOzMGpZGjwMjRYmmkSXMC7cBO
7cBS7cBC7cBC70kD42gwOXizOXi0OXiwOXiwONpcttYM0V4M0VIN0VIM0VIMUTGObBGDdNOD
dNSDdNCDdNCD1kQxiw8K6GcG6GkG6GEG6GEGqJ/dhxO3izO3i0O3O02Z4xO3G+sXqSXWrR9W
6T4s1nQarPhwWfCltayOVrQ1uGhcaRRYnXUTCkKkJNMHl9ayDULRNwUE2pIheOSRJLD3e1oH
jwg1ZcpWJbpgsYkzWKC70laSKShYxxItYduNqVaNKILG58miwOxpm0PUIWsG9IMmsO+dblAh
CykROFqIszhqVi+JEbWDf4NaV5rnt46Yjc2URYnOVrUqTI2sG+5LQ1Srj85WJFnhEpfqvxLd
y4/mDN2xw2N3lM4mVVVwJOi1qUph/sRzQl2XOnZ8y2NzyMUpn4ssdy8HEjnEHMC3V2PPvM2Z
Q2VGEBTSXRRGLJuiTOUSchJ8DP0VuxPuweqKi4IxV2xOQwulckjA0toTdofdK9EHznbpn+g9
cLfIHlnrEBc4d1vB0JdiMRPru5Lkhvujuyg8uS2XYMvsi/eTOlsT/KX43hymUsyEnc0IQTyb
g6KVOl8+uYl1Jiko5RIBcyrX5UiP+lsMMpjpK+4X4SPSP21u0TxH/yX6TgJvCmeNpJuImm2X
30IBKQJ2rdi7lpNAeoDXnroZVGhDNYjeVNnS4wuwmThyYXbzw0goJjcsA0gIqNvhdRODSHG8
6cGmOM1l6MIdYwr2ZY6wUXwzg0hhumnhpCTdZPDSFG8KfGmOM1F/MIdYwr/ZY6wGJetYwrCa
Y6wUXI0g0hhuWohpCTd5QDSFG8KiWJdI3biq6hXgN3HFMfiiWgN7VaMB2sHAIEYz+RZkAb2v
AjGYz+FZsAb2jEIDs5RQgTgNPCsE7ygMwmHHBsB284oRJwmHDReB28YIjfvJwHYzTYZoCs5x
wKk9xAdgNPmghuHHUCs5xkN89/gagNPm8Bv3IYCsZndsrzWq4/NGd/FoiIq+TL9WPbEeLGGj
4ihBYuYYcqLWV/Gmi+B9yung2iVl9LmVh+wfo+oSaJpjPI3L2J/t/XZf72pjoIlYIYmnECnW
iB88SMQkYiLpL+nPaMdf8S84SHKzvClkZ5ihpwY4xLqWukofcu/eQKxBP0egDl8uaaWjEYxF
mAWywEwzGmAN6wEwwHmwIEi5QvEvX9qqmTjnPAXZC+H1xspVgPCQpkRMHq+qZMTYSKzEoyZm
AGSzEQxamAaazEoybmAGizEQxcmAWqzEM5zBfk24OTvH/Nl6H9WaxQv93QzlAVi3Eww8mAKq
3EQz9mAVy3Eww+mAK63EQx/mwkEwJQlBOBMUwJgiDOBskwJ0mFOHgppq/UdA8IIQkKOBc8EI
QjMOB8sxJEIdcaWtx/KI64EIzHnAdC5ECkROtrXNKcsQRJnAVO5EITKnAVW5ECmWOBE8yJgk
YOhAZmTLbwedGCww33jN3cCiQOnAR25E4SPnAN+5E4SQnAVG6E4SRnAVO6E4SSnAVW6E4STn
ARe6E4SUnAVm6E4SVnAVu6E4SWnAV26E4SXnAR+6E4SYnARG7EmkyOBUc2JMCpdCjyanw40q
o1ygApuTgF3dChTenAK27EoQfnAV+7E4SgnAaG8ECiCPBSc4JMFJeChwinQg04JEIPeCBTkn
ACm8EClKPhR5uEgEhWCBToPAOKtEQxplAOStEwyqlAfatEIxrlARitEYwslADqtECjbLBBI3
SgG7WCUp3SgD/WCcI4SIQGuECkiLhg44SIcSuECnlLBy8vGECnrBhxzaQQcrGQiP1ARo7SAP
lpBkoJNgDjXCcp8SADnXa2jhZDx6ZAZmODQxuZALivEQwhZAGeLDQyVZAS+JDQzJZABeIDwz
9YQgEgJIDDYC0oATgHHYCsJBTQGWwEQTDmABewEwTEmAfmwEwExY1hBPmxypxFmAfywEwE0Y
jGL9TAnnPCYgDxXCEnPMBZIETgOjYCYicMjxlPMlYCU5ETgMpYCcYFTgDtYC84FTgLxYCMZG
TgE1YCTzNmAZyxEQxOmAO6xEwzPmktkPQZJfgzS+AIxRmALSyEwySmAeayEoxTmANiyE4wUm
AWqyEQzVmAWyyEoyWmYMGAFfZCEIMTgOjZCEoMTgEnZCEINTANrZChTbmAaezEQScmAFmzEw
TdmAGuzEQRemAO2zEQQfmAO+zEQRgmAOG0EIThmAOO0EQTimASW0EwTjmACe0EwQkmAGm0EQ
SlmAeu0EQQmmAG20EQSnmAS+0EwTomACG1EwQpmAWO1EQSqmAeW1EQQrmAGe1EwSsmASm1Ew
TtmACu1EwQumAa21EQSvmAe+1EQQwmAGG2EQTxmASO2EwTymACW2EwQzmAae2EQS0mAem2EQ
Q1mAGu2EwS2mAS22EwT3mAC+2EwR4mAeG3EQS5mAeO3EQQ6mAOW3EwT7mAWe3EIQ8mAGm3EQ
S9mAeu3EwS+mAB23EwQ/mAW+3EIQAnAWG4EIQBnAGO4EwSCnABW4EwSDnABe4EwQEnAam4EI
QFnAWu4EIQGnAK24EwTHnAe+4EwSInABG5EQRJnABO5EIQKnQosyJQkWOhgZBCIQi5EwxMnA
Gq5EwxNnQgX/dQC25EQTPnAF+5EYQQnATG6EEiiOBqc0JghkOBOs0JEONdCI4pTAHRdC4YqT
ALVdC45qTANZdCIZrTgCddCs4rTgChdCcYsTgKldCY4sTz5ynGMndCMJtTgLrdCYotTjxVCa
EBQDl6OBec3Jwk8OBes3Jgk+OB083JQiAPBMM4ppp+jAYwTgNFeCY4wzKO3kOeuXlTDeJjQi
nALW8EkhGPBO84JIDReC8YyTQGq8E4xlngMk5JwjNPBZozTgFfeCyQonAPG9EkhSPBec6JID
peC8Y1TQGa9EYxrngME7JwjZPhwp2TQGu9EoRunAP29EYTvngM87JgmgPBCM8JgniPB+c85n
QIbPGuU77QhmPlLktnAOKhs9oQKATfCyQ1nAdu+UqQ2eUwCa7QoR3nAH++E4Q4nAPG/E4S5n
ATO/EoQ6nwgs+Z1P9TmVYXvGwHuc6mhANT+h4tPY+yZym4HMgnEtOKOa7qVl/e0Gj/2+slrX
9UU5DibkY16yfTDn932uJataKvf/3VaAt1gjnKL+8HqMP18B/+v7/Hw2LvJa
}
Just to add that you'll notice there are significant differences if you zoom in but if you put another layer of the Mandy on top using my class "Field estimator" outside colouring in distance estimator "distance" mode and use a solid black "outside" with opacities set such that the black area only appears closer than a certain distance away from inside and then leave that layer on and turn the middle layer on and off to see the two different DE angle colourings you should see that the method I use matches the actual outline of the DE at the threshold set by the transparency in the top layer whereas the analytical angle is showing the angle based on true inside - obviously in 3D the former is a better option i.e. the DE angles and hence the normals should match the shape of the actual rendered solid not the shape of the true "inside". |
|
|
|
« Last Edit: November 21, 2009, 11:40:29 PM by David Makin »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #27 on: November 21, 2009, 10:34:36 PM » |
|
With DE I think it's quite simple to calculate normal vector because we can calculate some central differences or gradient of potential function. But what we can do when calculating of DE is impossible, for example for some strange non-linear fractal formulas? Now I know only one method. It is not so fast but gives very accurate and smooth normals (fractal details are also sharp). It is something like central difference but average for some area.
Maybe someone knows any other universal algorithm. I tried to found something in Internet but without result.
My delta DE distance estimation method can be used in such cases (provided you can get an accurate smooth iteration value) essentially the same way as using the analytical DE *except* you obviously can't use the analytical calculation for the normal you can only use either the solid surface found or the central difference method. Note that my current formula for UF uses exactly the same method to get the normals for both analytical DE and delta DE i.e. get the DE values at the points at the same distance from the viewpoint as the central point on adjacent rays giving 5 points including the central point, assume all 5 DE values are perfect *and* along the relevant rays and calculate the normal using the assumed surface points. |
|
|
|
« Last Edit: November 21, 2009, 10:39:53 PM by David Makin »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #28 on: November 22, 2009, 12:13:08 AM » |
|
With DE I think it's quite simple to calculate normal vector because we can calculate some central differences or gradient of potential function. But what we can do when calculating of DE is impossible, for example for some strange non-linear fractal formulas? Now I know only one method. It is not so fast but gives very accurate and smooth normals (fractal details are also sharp). It is something like central difference but average for some area.
Maybe someone knows any other universal algorithm. I tried to found something in Internet but without result.
My delta DE distance estimation method can be used in such cases (provided you can get an accurate smooth iteration value) essentially the same way as using the analytical DE *except* you obviously can't use the analytical calculation for the normal you can only use either the solid surface found or the central difference method. Note that my current formula for UF uses exactly the same method to get the normals for both analytical DE and delta DE i.e. get the DE values at the points at the same distance from the viewpoint as the central point on adjacent rays giving 5 points including the central point, assume all 5 DE values are perfect *and* along the relevant rays and calculate the normal using the assumed surface points. Just to add that to get an accurate smooth iteration value for more esoteric formulas e.g. involving transcendentals or conditionals then see here: http://www.fractalforums.com/3d-fractal-generation/re-true-3d-mandelbrot-type-fractal/msg8714/#msg8714In even worse cases then you can use exponential smoothing (with appropriate scaling adjustments) in the delta DE method as an alternative to iteration smoothing, the only real drawback? with that is that it is generally a noticeably different outline to either solid on iteration or solid on DE based on potential/iteration. |
|
|
|
« Last Edit: November 22, 2009, 12:27:56 AM by David Makin »
|
 Logged
Logged
|
|
|
|
|
gaston3d
Guest
|
 |
« Reply #29 on: November 23, 2009, 10:18:45 PM » |
|
Hi, all methods based on gradient requires smooth potential function which is very hard or impossible to get when formula function is true/false only. I use method like this (2D equivalent, see picture): 1. raytrace R(t) by small "dt" values (~1e-3) until hit the object (blue line), then fine tune hitpoint using bisection method until |R(t1)-R(t2)|<epsilon (~1e-9) 2. create small "cube" around hitpoint getting four points ABCD (8 points in 3D case); parameter N~100 gives size of the cube around ~2*1e-7 3. search points P1, P2 on the surface - bisection between proper point pairs (one "in" one "out"); in 3D case, it may sounds weird, there can be 12 points (not belonging to the same surface...) 4. having set of points on the surface calculate normal as average of partial normals (perpendicular to green lines, or triangles in 3D case) "cloud" set of points on the surface can be used in another methods: 1. approxiamte points by ordinary plane using least squares method; having plane equation, normal vector is trivial (hard...) http://www.infogoaround.org/JBook/LSQ_Plane.html2. make local analytical parametric surface R(u,v) and calculate partial derivatives (dR/du, dR/dv) that leads to exact normal vector (very hard I think...) http://en.wikipedia.org/wiki/Parametric_surface#NotationI've used method described by David in Reply #1 some time ago and results were fine (x & y +/- 0.25 of a pixel). It's not necessary to raytrace 4 rays from camera location, you can use ray distance "t" from central point and trace surrounding 4 rays forward or backward. One disatwantage is when central point is on the edge of the object, then one of additional points can miss the fractal and you raytrace till hit the bounding sphere or other far part of the object. |
|
|
« Last Edit: December 04, 2009, 08:35:27 PM by gaston3d »
|
 Logged
Logged
|
|
|
|
|


















