|
Dinkydau
|
 |
« on: February 24, 2012, 02:11:03 AM » |
|
Hello everyone,
I like fractals a lot but I've only recently started to wonder what exactly is going on. I was wondering to which extend there is insight in the shape of the mandelbrot set. I have been asking myself many questions that I couldn't answer myself lately regarding this.
To understand the mandelbrot set better I have tried to find more information, but there isn't much information available about this or it's too difficult to understand for me. I know complex numbers, the mandelbrot function, how it is plotted in the complex pane, how the colors are generated and by simply exploring I have gotten to know some patterns in the mandelbrot set. But that's where it ends. It's only very basic things that I know while everywhere on this forum people are already discussing, what is to me, incomprehensible maths about 3d and 4d fractals. Probably the 2d mandelbrot set has been thoroughly investigated by many already but I'm still at that stage.
For example, you can see that the mandelbrot set for a significant part consists of "circles". While at some points they really look like circles, it depends on where you zoom. They're clearly not all perfectly round. Are there actually any circles in the mandelbrot set?
It looks like the largest of the circles in the mandelbrot set is connected to the weird shape on the right at -0,75, and connected to the next circle on the left at -1,25, meaning the diameter of the circle is 0,5. Is there any proof of this? Do all "circles" in the mandelbrot set have such a round diameter? Is there a pattern, a relationship between the sizes of all the circles?
On the real axis, from -2 to 0 no values go to infinity when iterating the mandelbrot function. Am I right to conclude that this means that on the antenne of the mandelbrot set lie infinitely many mandelbrot sets together forming the line?
Where does the mandelbrot set "end" at the real axis? It's obvious that it reaches from -2 to some positive value, but I wonder what that value is. Can it be defined?
Is there a method to calculate where a small mandelbrot set lies at a certain zoom level?
Are we 100% sure that the mandelbrot set is actually a fractal? Because its definition doesn't involve anything I would expect to turn out to be a fractal. I've started to question this after I read that the Riemann hypothesis (which is unrelated to fractals, just an example) is considered not proven even after some people used a computer to calculate billions of values and they were all according to that particular hypothesis. The hypothesis was still not tested for all values, which are infinite. So, are we really 100% sure that the mandelbrot set is a fractal, and how do we know that? If this has been investigated, it will probably give a huge insight in why the mandelbrot set looks like what it looks like too.
If any of my conclusions do not make sense to you I can explain them further.
|
|
|
|
« Last Edit: February 24, 2012, 02:15:34 AM by Dinkydau »
|
 Logged
Logged
|
|
|
|
|
taurus
|
 |
« Reply #1 on: February 24, 2012, 09:41:09 AM » |
|
On the real axis, from -2 to 0 (actually 0.25) no values go to infinity when iterating the mandelbrot function. Am I right to conclude that this means that on the antenne of the mandelbrot set lie infinitely many mandelbrot sets together forming the line?
in fact along the x-axis (where the imaginary components are zero) is one of the most interesting parts of the mandelbrot set. the image below (taken from wikipedia) shows the correlation between the mandelbrot set and the feigenbaum graph. you see there, that the boundary values of the mandelbrot iteration (for all bi=0) converge to one or more values. within the antenna the iteration goes chaotic. you see also, that the antenna is at full length part of the mandelbrot set (as long as bi=0) so i guess your assumtion about the antenna is correct as the feigenbaum graph is extraordinary important to chaos theory this correlation is the main port between fractal geometry and chaos theory.  |
|
|
|
« Last Edit: February 24, 2012, 10:29:51 AM by taurus66 »
|
 Logged
Logged
|
when life offers you a lemon, get yourself some salt and tequila!
|
|
|
Mrz00m
Fractal Lover
 
Posts: 204
|
 |
« Reply #2 on: February 24, 2012, 03:54:22 PM » |
|
http://www.miqel.com/fractals_math_patterns/visual-math-mandelbrot-magic.htmlhere is some good info about shapes in fractals. the most interesting thing it sais is the M-set has been proven to be the longest continuous single 2d line in maths, as it is essentailly just one boundry line. Which means that it is a pretty special formula/class of formuli. I dont know if i believe that it's infinity is the only and largest infinite line formula in maths, but it's intersting. The shape of the M-set seems to be one of those fundamental shapes in our universe that we are not presently qualified to comment on! Why are there 132 elements of different sizes and shapes that combine into millions of types of rocks, stars, and enzymes etc. These are the patterns of the natural chaos/complexity of the cosmos in it's present state. i think that's all we can say about these shapes! our concept of shape has not evolved enough to logically compare things like the mandelbrote to anything in our tangible reality. same with spiral galaxies etc. It's inherently a different class of formula from any other ones in mathematics, it is simpler, it doesnt rely on any angles, shapes, or any object oriented stuff. it's results are more complicated. the formula is very abstract and untangible, a perverse experiment by a genius mandebrot. it simply a number bending back into a square of itself or something. the fact it is an abstract logarithmic function that happens to bend back into itself in a small space means it has a kind of logarythm, pointy, shape, with large curves representing the lower expnential values before the curve picks up, and the infinitaly small details correspond to the distant reaches of the exponent. it's kindof a perfect hybrid between a circle and an infinitely spikey exponent, the circle folds over itself into a bear shape and the spikes go into the distant spirals, same as when some 2 line maths formulas produce for you figure of 8 shapes, or a doodly but this one is infinite... a small formula like a snail shell shapes, just an infinitely folder over snail shell, in 2d. thats my 2c 
|
|
|
|
« Last Edit: February 24, 2012, 04:02:32 PM by Mrz00m »
|
 Logged
Logged
|
|
|
|
|
Dinkydau
|
 |
« Reply #3 on: February 27, 2012, 02:54:32 AM » |
|
Thanks for the information
|
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #4 on: February 27, 2012, 04:57:07 AM » |
|
"Are we 100% sure that the mandelbrot set is actually a fractal?"
To be picky it isn't a fractal. Its border is a fractal. The set itself is the black bit which has an area. The border is a fractal by most definitions.
To me the most interesting feature of the mandelbrot set is that it is universal. So you can alter the formula by rotating, scaling or translating every iteration and you still get a resulting mandelbrot set. This roughly describes why the mandelbrot set pops up in many different formulas.
No other fractal is universal, it is completely unique to the mandelbrot set, actually, to the multibrot sets (Z2+C, Z3+C, .. Zn+C).
It is as though these multibrots are the foundational shapes in some way. Just like the natural numbers are foundational to arithmetic.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
taurus
|
 |
« Reply #5 on: February 28, 2012, 09:39:36 PM » |
|
"Are we 100% sure that the mandelbrot set is actually a fractal?"
To be picky it isn't a fractal. Its border is a fractal. The set itself is the black bit which has an area. The border is a fractal by most definitions.
for sure we can be so picky. But we can also be so picky, that the borderline does not fit one important definition - the namegiving dimension is not fractal. with 2 it is integer. i can't say, that i understand, how a not area-filling curve can have a haussdorff dimension of two. and it's still not clear, if it has an area at all - but at most it is finite. i think we could count a lot more oddities without finding an end, but i guess we are in common, that this piece is still one of the most mysterious parts of math. for me as a non-theoretician the mandelbrot set is not only a fractal, it is the mother of all fractals. |
|
|
|
|
 Logged
Logged
|
when life offers you a lemon, get yourself some salt and tequila!
|
|
|
Mrz00m
Fractal Lover
 
Posts: 204
|
 |
« Reply #6 on: February 29, 2012, 08:06:33 AM » |
|
and it's still not clear, if it has an area at all - but at most it is finite.
Why wouldn't a mandelbrot set have a precise area formula same as a circle? the formula for PI is "recursive" and there must be a constant like PI for fractals... i am amazed that there isnt a formula for it, surely someone will find one some day. Perhaps they should add it to the X-prize style maths challenge. i circle doesnt really have an area because PI is infinite, and M-set should be the same? Haven't they just computationally measured the area of the m-set to a few hundred decimals by counting the black pixels at crazy zoom levels? |
|
|
|
« Last Edit: February 29, 2012, 08:13:44 AM by Mrz00m »
|
 Logged
Logged
|
|
|
|
|
taurus
|
 |
« Reply #7 on: February 29, 2012, 08:55:34 AM » |
|
Why wouldn't a mandelbrot set have a precise area formula same as a circle? the formula for PI is "recursive" and there must be a constant like PI for fractals... i am amazed that there isnt a formula for it, surely someone will find one some day. Perhaps they should add it to the X-prize style maths challenge. i circle doesnt really have an area because PI is infinite, and M-set should be the same?
sorry, that i spoke unclear. i was talking about the boundary line of the mandelbrot set. it has the dimension two and might not have an area at all... Haven't they just computationally measured the area of the m-set they have. it is: 1.506 591 77 don't know the unit. wikipedia remains silent. |
|
|
|
« Last Edit: February 29, 2012, 09:05:35 AM by taurus66 »
|
 Logged
Logged
|
when life offers you a lemon, get yourself some salt and tequila!
|
|
|
|
Pauldelbrot
|
 |
« Reply #8 on: April 26, 2012, 02:40:20 AM » |
|
The cusp of the elephant valley area is at exactly 0.25. Also the biggest bulb attached to the core of the set is in fact a perfect circle, and is probably the only part that is exactly circular. It's centered on -1 and has a radius of 0.25. This can be proved but requires digging into calculus and dynamical theory a bit.
The antenna is, as you surmised, essentially made of minibrots. Every point on it is either inside a minibrot or a "point of accumulation" of minibrots -- that is, given any point P on the antenna not inside a minibrot and any ϵ > 0 you can find a minibrot inside a circle of radius ϵ about P. In fact the same is true of any Mandelbrot set point along any dendrite, seahorse spiral, etc.
|
|
|
|
|
 Logged
Logged
|
|
|
|
makc
Strange Attractor
  
Posts: 272
|
 |
« Reply #9 on: March 20, 2013, 07:57:07 PM » |
|
bumping the thread, with my orbits explorer:
<a href="http://swf.wonderfl.net/swf/usercode/3/3b/3b95/3b95ba3061861169c86ea897e54f783a01526847.swf" target="_blank">http://swf.wonderfl.net/swf/usercode/3/3b/3b95/3b95ba3061861169c86ea897e54f783a01526847.swf</a>
maybe not the best way to visualize orbits, but the best of what could be done in 30 minutes
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Syntopia
|
 |
« Reply #10 on: March 20, 2013, 09:09:20 PM » |
|
Nice! I also made an similar orbit viewer (in WebGL) a few weeks ago: 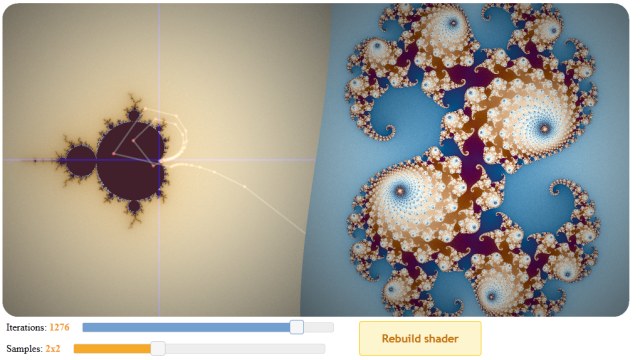 Available here: http://hvidtfeldts.net/WebGLSet/orbit.htmlNo splines, but you can zoom in realtime, if you have a fast GPU :-) |
|
|
|
|
 Logged
Logged
|
|
|
|
makc
Strange Attractor
  
Posts: 272
|
 |
« Reply #11 on: March 20, 2013, 10:04:43 PM » |
|
yes I thought about the zoom too, but then you need separate unzoomed view to see the orbit.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #12 on: March 20, 2013, 10:34:29 PM » |
|
Sorry for typos just using the tablet. . Very good thread here, i can not promise anything but i am working on at least a nice overview on what the mandelbrot set is and how the julia set belongs to it i have nothing to show yet but in my research i found another question to think about, which is: Why the heck is the mandelbrot symetrical on the x axis? The points are behaving completely differently but bail out at the exact same iteration step next issue will be very insightful at least  The other things you already scratched the surface of i can answer at least some @taurus space filling curve is a bit unprecise naming but when you watch the mathematical definition of how a space filling curve is defined you will see that this just means that every sub part of this curve has to posess infinite lenth as well the mandelbrot set is somehow the mother of fractals because of its beauty but for sure not the first i just spit out everything in my head right now i wonder qhy the visualisation method is not used to understand instable behaviour of numerical functions especially for fluid dynamics, what the escape time method is basically visualising is the speed of growth the mandelbrot set is created by an awesomly beautiful simple formula, some of you already heard from the affine transformations which are used for the plain ifs fractals like zhe fern for example as i never grt tired of explaining is that hence complex multiplication is a rotation and a scaling it is the addition qhich completes the simple affine transforms which are rotate,scale and translate tglad with his mamdelbox incorporated two more transforms wich are inversion and reflection, and put them in a equally beautiful fomula. . . So regarding that chaos occurs very fast like in the logistic equation qhich formulates population growth or the three body problem from physics it is a representand for the beauty of complexity that occurs from simple processes uff, i hope to finish my introduction to the mandelbrot set before the contest starts and before my next trip to mexico i will return talking about the mandelbrot set all the time because it is full of an awesome whole lit of interesting aspects many of them still just lay around and are not yet appkied to more usefull processes and we fractal fanatics are often just smiled at but you will be astonished what universal insight will pop out from this object phew . My 2 c  |
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|
Syntopia
|
 |
« Reply #13 on: March 20, 2013, 11:20:12 PM » |
|
Why the heck is the mandelbrot symetrical on the x axis? The points are behaving completely differently but bail out at the exact same iteration step
I think the orbits are simply mirrored?  Here is a orbit viewer for the mirrored point as well: Available here: http://hvidtfeldts.net/WebGLSet/orbit2.html |
|
|
|
|
 Logged
Logged
|
|
|
|
|
cKleinhuis
|
 |
« Reply #14 on: March 20, 2013, 11:46:01 PM » |
|
Thank you for that syntopia i will examine your orbits viewer and perhaps use it as well but my question just goes a little deeper: Why are they mirrored? Consider the pure imaginery points i and -i in the iteration process when squared they both land on the -1 real position so, what happens with the translation? Both points are moved one along the y axis to -1,1 for the point started on positive i and -1,-1 for the point started on negative i it seems obvious that their positions are just mirrored but isnt it quite interesting qhy this holds true for even such 'odd' locations whose distance to zero is square root of 2?? We see that they are symetrical but do we really understand why it holds true for every position on the plane? It might aound a bit weird to bring it up, and for an expert mathematiciand it might be really trivial but i find it quite fascinating that the multiplication itself is quasi symetrical on the x axis, for the translation it is obvious but in my eyes not so clear for the rotation thing where we are at the pi circle definition  it is mirrored for sure, but quite puzzling for me  |
|
|
|
|
 Logged
Logged
|
---
divide and conquer - iterate and rule - chaos is No random!
|
|
|
|


















