since those numbers don't actually grow all that fast, you could also define n over k recursively via integer addition, using a "dictionary" (a dynamically extended lookup table) to keep that implementation reasonably efficient without using big num operations.
Just define a bunch of relations you'll need:
binomial(0,0) = 1 // base case
// (1,k) for all k - you could even ignore the base case since it also is defined by this
binomial(n,0) = 1
binomial(n,n) = 1
//(2,k) and (3,k) for all k
binomial(n,1) = n
binomial(n,n-1) = n
//out of bounds binomial coefficients
if k<0 || k>n => binomial(n,k) = 0
//all other possible cases, without any multiplication at all
binomial(n,k) = binomial(n-1,k-1) + binomial(n-1,k)
Technically you only need the base case (0,0), the out of bounds case k<0 or k>n, and the recursive addition to really catch them all, but the other couple rules up there are so simple, I don't see why you wouldn't add them in anyway.
A naive implementation of this will suffer from the same issues, a naive implementation of recursive Fibonacci numbers or a naive recursive factorial would suffer from, so if you go this path, I highly recommend dynamically generating a lookup table as you go, to keep down calculation times.
If you are concerned about the memory consumption of such a table (which you really shouldn't be - it shouldn't be a big deal to store numbers of those sizes), you can employ one extra rule to essentially half that memory consumption by using the rule
If k>n/2 => Binomial(n,k) = Binomial(n,n-k)
All this together should give you a pretty acceptable, reasonably fast implementation of Binomial(n,k) - The largest of Binomial coefficients still grows rather quickly, though. With your standard unsigned (32-bit) int precision, you'd get up to Binomial(18,9) = 48620 with this. Binomial(19,k) will start to see problems once again. However, you'll find yourself pretty rarely in a situation where you actually need to use anything of dimension 19.
The largest Binomial Coefficient grows with roughly
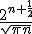
, while the general asymptotic growth of any binomial coefficient is about
^{k-n-\frac{1}{2}})
.
Another thing you could try is to figure out precisely what multiplications you do not actually care about, to also avoid overflow.
12!/(6! (12-6)!) = (12*11*10*9*8*7*6*5*4*3*2)/((6*5*4*3*2)*(6*5*4*3*2)) =
(12*11*10*9*8*7)/(6*5*4*3*2) =
(2*11*2*3*1*7) = 11*7*3*2
2 = 924
This would require some kind of implementation of rationals where you can reduce them to their simplest form symbolically, before even executing any numeric multiplication. That could be interesting and worthwhile in its own right but it's probably also beyond what you are trying to do here. In the end, it would probably be slower and it'd suffer from the same limitations as the recursive definition above.
All that being said, I'm with Roquen that 12! is more than sufficient for your needs. Just work on other parts. If needed, you can convert to bignum later down the line just fine.
Appendix: Full Form of the Asymptotic Behavior of the Largest Binomial Coefficient, Corrected for Even and Odd Values for n:
^{-\lceil \frac{n}{2}\rceil -\frac{1}{2}} \left(\lfloor \frac{n}{2}\rfloor +1\right)^{-\lfloor \frac{n}{2}\rfloor -\frac{1}{2}} \: e^{\frac{1}{360} \left(-\frac{30}{\lceil \frac{n}{2}\rceil +1}+\frac{1}{\left(\lceil\frac{n}{2}\rceil +1\right)^3}+360 \lfloor \frac{n}{2}\rfloor -\frac{30}{\lfloor \frac{n}{2}\rfloor +1}+\frac{1}{\left(\lfloor\frac{n}{2}\rfloor +1\right)^3}-360 n+720\right)+\lceil \frac{n}{2}\rceil } )
geometric spirals
Mandelbulb3D Gallery
October 25, 2010, 09:48:32 PM
Dilber MC Theme by HarzeM