Geometric Algebra, Geometric Calculus

[kram1032]

Thanks for those contributions

At this point I am just experimenting.
I'm not even concerned with the outer product right now. As said, I only experimented with the geometric product.

However, you are right about the outer product being changed quite significantly.
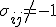
As I already showed in my previous post, in using a , you actually don't even get a pure antisymmetric part. You get both a scalar (which is symmetric) AND a(n antisymmetric) bi-vector component if you use the standard definition of a wedge product.

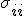
I did not define the inner product as anti-commutative. I already showed how , i.e. the factor you get from exchanging a base-vector with itself, must always be 1. Hence, it is symmetric.

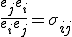
, that is correct. It's a nice alternate method to denote it.

Your orthogonality remark is topical: That's actually why I am investigating this direction.
You do not actually need an orthonormal basis of vectors. You can just have n completely arbitrary base-vectors for an n-dimensional space. They can lie at completely odd angles to each other. The only limitation is that they must not be linearly dependent on each other.
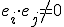
That would just be a generalization. Nothing unheard of. In fact, in certain cases, like, for instance, in triclinic crystals, it's actually more natural to describe your coordinates in such a non-orthognonal and perhaps even non-normal base.

However, I have found the problem with my problem now. I did nothing wrong in my calculations, but I interpreted it wrong:

The offending equation was the following:

So that means:

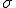
I previously simply assumed, that that means, could only be 1 to fullfill this equation. However, all that is required, in accordance with a different equation I already got before, is this:

and

This is required for sake of consistency.
Thus, the whole system reduces again to precisely what we already had before, as far as commutativity goes.
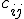
All that is left is our , which now are restricted a slight bit further too.

In particular:

From there we could get:


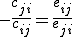
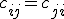
This is definitely consistent if we just set . I'm not absolutely certain right now, that this is the only consistent concept, but it might be.
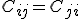
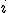
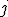
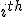
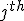
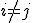
If it turns out that this is the unique solution, we'd essentially have some symmetric matrix of which each and stands for the additional factor of a geometric product of the and base vectors. - This would essentially be the metric tensor of our given system. The main diagonal would give the usual signature of the system, while all the other values correspond to rotated components. They only occur, if the system is not orthogonal.

As said, I'm not yet fully convinced, that this is the only solution here, though it's not unlikely.
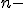
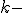
But if it is, we'll still have to look into what happens for other vector multiplications. For instance, what happens if we multiply a vector and a bi-vector or, essentially equivalently, three vectors? Things can become really complicated really quickly, but most certainly, a pattern for multiplying with vectors should appear sooner rather than later.

[hermann]

if the do not form an orthogonal base I think you have to play the game with covariant and contravariant vectors and you have to define what your metric is.

being the spat product!
I have not tried to write this down with geometric algebra or do we have a source where such thinks are discibed?

[Roquen]

The geometric product is defined as follows:
<Quoted Image Removed>

To be anal, no it's not defined that way...the product rules for the basis elements define the full product.  This is an identity to show these two specific partial products are related to the product.

[kram1032]

Not really.
You could define just as well as you could define

It's almost the same thing as defining:

versus

In both cases I'd argue that the second version is the more fundamental one, however, there is not actually anything wrong with doing it like in the first version. You just have to pick.
One of the two things is defined, and the other is derived. Which one matters very little.

Really, this can be expressed as:



and



respectively. In either case it takes simple algebraic manipulations to show that these are correct.

[hermann]

Thanks Kram,

I am a little tired and exhausted this evening so I can work it out in detail.
But I think your construction has something to do with the metric tensor which plays an importend role in general relativety.

http://de.wikipedia.org/wiki/Metrischer_Tensor
http://de.wikipedia.org/wiki/Krummlinige_Koordinaten



Hermann
P.S may be I can work out the details the next days.

[kram1032]

Indeed it does, and I already said so

This would essentially be the metric tensor of our given system.

Btw, why do you link to the German Wikis? - Obviously, you and I know German. But I think the largest part of the community, by language, actually is natively English speaking and doesn't understand German either well or at all.

http://en.wikipedia.org/wiki/Metric_tensor
http://en.wikipedia.org/wiki/Curvilinear_coordinates

(Also, very often, English wikis are better than their German counterparts. - Although the German Wikipedia is amongst the best. Especially in Chemistry it actually frequently beats the English one in my experience. Still, usually, English is better, and it's more universally understood here )

[kram1032]

http://wavewatching.net/2014/10/27/the-unintentional-obsfuscation-of-physics/

[kram1032]

Here's another wild idea. I didn't actually test it much, yet. Could be complete nonsense.
However, as we have seen, only had the following condition on it: .
I assumed sigma to be a scalar. But what happens if you let it be its own vector?
For instance, starting with a 2D Geometric Algebra with positive signature:



This gives the solution:



Anything that sticks to those parameters,
- is its own inverse
- should be a plausible definition of .

This kind of extension can become very complicated very quickly though. It remains to be seen whether that would even be a valuable addition.

[kram1032]

Here is an awesome paper: Vector Analysis of Spinors (pdf)
It's pretty simple to follow as far as I've seen.
I haven't even reached the meat of the paper yet (I'm just about to get there), but already what happens before that is pretty nice.

It's not very well checked though. I found a few errors: Two times, early on, there is a which should be a , later down the line, a in an exponent is supposed to be an and one of the worst errors I found thus far is falsely calling Heisenberg Heisenburg.

There also is this flash video talk:
http://www.worldsci.org/php/DimDimFlashViewer.php?id=336
I wish the quality would be a bit higher. He sadly isn't a great talker: He's very clearly nervous. Though it's still a good talk.
The slides for that talk can be found here http://garretstar.com/nfmtalk2010/AMS-MAA2013.pdf

[kram1032]

Apparently, this paper of his is more recent:
Geometry of Spin--particles

He apparently was a direct grad student of Hestenes.

[hermann]

Interesting links!

I hope I have more time next weekend to look on it in detail.

Hermann

[kram1032]

It's actually pretty timely: My recent experiments partially aimed at answering exactly the questions he answered in those papers (if not in full generality). The gist of his work appears to be to unify matrices and Geometric Algebra to the point where you can do everything with GA.
He's focusing heavily on idempotents (values which have the property, that . For the reals, this only works with and ) and nilpotents () and, very importantly, he establishes, that such idempotents pretty much are the Geometric Algebra version of Eigenvalues.
This is something I have pondered about for a while, actually. Eigenvalues and Eigenvectors are, like, THE most important thing behind matrices. If you have them for a given matrix, you can apply /any/ analytic function to those matrices.
Now what is left for me to figure out is: what about non-square matrices, and how to fully translate arbitrary tensor algebra into this format?
It certainly must be possible, by way of the underlying isomorphisms.
Sadly, he only touches on square matrices, focusing on 2x2- and 3x3-ones, not really saying much about nxn- and saying nothing about nxk matrices.
However, a part of what he did hinted at possible extensions for such arbitrary cases.

Obviously, an nxk matrix represents an either under- or over-determined problem. I was wondering how well GA could deal with such cases. I haven't found a whole lot on that yet.

And the other thing, tensor-algebra, is because we learn it that way at university. Coordinate transformations from one frame to another appear to be half of the bread and butter of a physicist. And even if Tensor-algebra is highly cumbersome at times, especially once you get into Co- vs. Contravariant stuff (damn that stuff is easy to mix up. Luckily the distinction isn't always important), it's still really powerful.
I've seen demonstrations of specific cases, but I haven't yet seen a generic 1:1 translation of something expressed with arbitrary tensors to something expressed in some fitting Geometric Algebra, even if that is, alledgedly, completely possible.

Once we can have arbitrary-dimensioned tensors fully translated in GA and back, we can truly compare the two approaches. (Thus far, what I've seen is mostly "very promising", to the point where I'd love to just do everything this way, but no complete, rigorous, exhaustive 1:1-translation)

[hermann]

I found this fine article on Bivectors in Wikipedia:
http://en.wikipedia.org/wiki/Bivector

Hermann

[kram1032]

Thanks Hermann
There's also http://en.wikipedia.org/wiki/Multivector

Meanwhile, just for fun, idempotents in spherical coordinates:



with



then
You could substitute that back into the orignal, but I think it's nicer to look at with that condition. As long as and , we are looking at an idempotent, squaring to itself.

[Roquen]

In both cases I'd argue that the second version is the more fundamental one, however, there is not actually anything wrong with doing it like in the first version. You just have to pick.
One of the two things is defined, and the other is derived. Which one matters very little.

Like I said:  I was being anal.  But if you define in terms of the partial products then number of axioms explodes.  The simplest definitions wins.