Geometric Algebra, Geometric Calculus

[hermann]

Octonions are not a Clifford algebra, since they are nonassociative.

[kram1032]

Oh, good point. Interesting.
That raises the question of how geometric algebraic "Octonions" (as proposed by me) compare to actual Octonions.

[hermann]

A good source on octonions in the internet is the page of John Baez:
http://math.ucr.edu/home/baez/octonions/

May be I have some time next weekend, so that can I do some colouring on my geometric algebra tables. Also having different signatures may be helpful.
http://www.wackerart.de/mathematik/geometric_algebra.html

Hermann

[hermann]

I found this link:

Cayley-Dickson Hypercomplex Numbers Up to the Chingons (64D)
http://www.mapleprimes.com/posts/124913-Visualization-Of-The-CayleyDickson

Hermann

[kram1032]

I've been playing around with general non-commutative multiplication lately, trying to push geometric algebra as far as possible, but I ran into an unexpected problem.

Say you have your n base-vectors .
Assume, multiplying them is non-commutative.

However, they are proportional to each other, differing only by a scalar factor which commutes with everything:

From that first equation we also get

I.e. base-vectors always commute with themselves.
(Alternatively, the equation could also trivially be solved by setting which would mean, that the given is a null-vector, i.e. its magnitude is 0.)

Furthermore, multiplying two base-vectors together gives rise to a bi-vector, which also is assumed to be proportional with yet another commutative scalar :

etc.
That's probably all you can get out of just two indices. It becomes significantly more complicated once you get to three different indices.
Let's, for now, look at two different indices, one of which is duplicated. With that setup, there are three possibilities.






That last equation is a problem. There are three solutions to that equation:

• - that'd be pretty useless
• - in this case, is null
• - that would mean, all base vectors commute. ⚡

This is weird. Either there is a significant error with how geometric algebra is setup (In normal geometric algebras, , a possibility which I just demonstrated to lead to a paradox), or, which is a lot more likely, I made a major oversight somewhere in this. If somebody sees a problem, please point it out.

[hermann]

I've been playing around with general non-commutative multiplication lately, trying to push geometric algebra as far as possible, but I ran into an unexpected problem.

On the first view I think you are mixing things you shouldn't mix.

Basicly in geometric algebra you have three products:

• The inner product
• The outer product
• And the geometric product

The inner product is commutative! The outer product is anticommutative!
Now you define the inner product as anticommutative?
In geometric algebra you have to be very carefully if you multiply from left or right. (All so when producing the inverse).
Also take care with scalars.
Be carefull in geometric algebra you have different products! Don't mix them in a way you are trained for products in school.

Hermann

[kram1032]

I was actually using the geometric product.
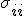
The geometric product of a base vector with itself is commutative (it's what the inner product gives you, and in fact it must be in the way I framed it above: is easily shown to always be 1, i.e. changing order does not result in sign change, i.e. it's commutative.), but with another base vector it's anti-commutative (xy = -xy etc.), which is the wedge-part of the product.
And scalars are completely commutative.
That's what I was assuming here. Or at least I was trying to.
I still must have made some error of that kind somewhere in there. But I can't really spot precisely where.

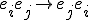
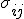
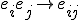
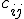
Basically, all I did was generalizing two things in Geometric Algebra to support arbitrary scalars: Switching (geometric) multiplication orders of base-vectors results in a swap-factor and (geometrically) multiplying two vectors results in another scalar factor which is essentially the signature, except I have used it on all base-vectors, not just ones of equal index. 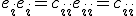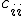(Normally, the signature would appear like this: ; where simply is the signature for that particular vector. I have added the possibility for giving mixed vectors such a signature factor as well.)

Nowhere in this am I even using the scalar product or the wedge product, except for where they happen to align with the geometric product.

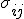
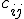
All I was trying to do is to see for which instances of and this is consistent; if, perhaps, this only even consistently works for and
I.e. whether this only works for the conditions we already know about (swapping unequal vectors anticommutes, swapping equal ones commutes, only base 1-vectors get an additional factor through signature) or whether there are more general situations.

Now it would be no problem if what I showed was, that only what we already do is allowed, but if I made no mistake (and I probably did), it means that not even that case is allowed.

Edit: Tex doesn't work well with the notation I used up there in c. What I was trying to convey is that c could have an arbitrary list of indices in general, for products of arbitrary n-vectors with arbitrary k-vectors. I wasn't quite sure how else to depict that, but this method using products clearly doesn't work all too well.

[Roquen]

Partial products are defined from "the product"...a la from Lie algebra.  (ab-ba)/2, (ab+ba)/2...toss in ops like conjugates to define more.

[kram1032]

I am aware.
Here:



Geometrically multiplying a base vector with itself is the same as the scalar product of that base vector.



If (as it is for "normal" GA), this would become 0.


If (as it is for "normal" GA), this would become .

Geometrically multiplying two different base-vectors with each other is the same as the wedge product of those vectors (or at least it would be if , as it normally is)

Throughout the whole thing I was using the geometric product.
The only two differences are that I am allowing for some arbitrary additional scalar factor appearing even after multiplying vectors geometrically, which are not the same (), and that I'm allowing non-commutative multiplication to result in yet another arbitrary factor ().

[Roquen]

I wasn't clear...that was a reply to hermann

[hermann]

can be seen as a symbol for the area spanned by the two vectors ,

It is an area with an assigned orientation.

may give a different orientation and a different area!

If you first move the distance and then the distance you should end up at the same point as if you move and then the distance . This is not the case if you multiply it with an arbitary scalar .
I think you have changed the basic properties of the outer product a little bit too much. Or do you have a meaningfull geometric interpretation in the plane?
In many physical theories path independence is very imortant. I have the impression, that this property gets lost when you define an outer product in this way.
I have not inspected the algebraic structres in detail may be this can be interesting.

[hermann]

The geometric product is defined as follows:

It contains a commutative part, the dot product or inner product and the anticommutative part called wedge product or outerproduct.
If you define the inner product also anticommutaive or with a factor you get something like this:


Hermann

[hermann]

I think a Lie-Algebra is also close to this issue:

But I am not an expert in Lie-Algebra.

[hermann]

What about:

using the geometric product?

[hermann]

Ortogonalty of the base vectors requires:

if i and j are not equal!