
At first, this looks like a tear in space, opening onto a strange new world.
There is a strange new world, alright: the world of Matchmaker, a two-parameter family of rational maps capable of generating arbitrary pairs of quadratic Julia sets, intertwined.
A technical explanation follows.
Freely redistributable and usable subject to the Creative Commons Attribution license, version 3.0.
Detailed statistics:
Name: Portal II
Date: February 8, 2009
Fractal: Matchmaker Mandelbrot set
Location:
b-plane,
a = 0.53256 + 0.31163
iDepth: Very Shallow
Min Iterations: 1
Max Iterations: 1,000,000
Layers: 4
Anti-aliasing: 3x3, threshold 0.10, depth 1
Preparation time: 1 hour
Calculation time: 2 days (2GHz dual-core Athlon XP)
There is a strange new world, alright: the world of Matchmaker, a two-parameter family of rational maps capable of generating arbitrary pairs of quadratic Julia sets, intertwined. Technically, it has two critical points, and so depending on the parameters there may be zero, one, or two finite attractors. Moreover, the finite attractors bifurcate independently, so any two connected quadratic Julia sets can be forced to tile the entire Riemann sphere together.
I constructed Matchmaker by starting from the map
 = \frac{z}{b(z^2 + 1)})
, which Mandelbrot himself studied and which also has two critical points. The critical points of
f(
z) have complementary fates, which leads to three possible behaviors: no finite attractors; two finite attractors that are rotated images of one another; or one finite attractor that is invariant under a 180 degree rotation and that captures both critical points. The latter divides into two cases, the attractor is the fixed point zero and the attractor is an even-length cycle.
It is important to note that infinity is not a critical point or an attractor here. It is a preimage of zero, and since
 = \frac{1}{b})
it is repelling for
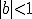
. (In Matchmaker, this becomes a more irregular shape and the fixed point moves off of the origin.) For these points, the Julia set contains both infinity and zero. Since
f(
z) is an odd function, it is rotationally symmetrical as well, and has two copies of the same quadratic Julia basin entwined, typically spiraling about zero and infinity, for parameter values that yield attractors. Its Mandelbrot set is a circle containing internal Mandelbrot buds, along with a "foam" of minibrots amid points for which there are no attractors. The Julia sets are interesting; the Mandelbrot set is difficult to visualize and is fairly boring (no seahorses, etc. can be seen with any of the visualization tricks I know).
I decided it would be interesting if instead of entwining two copies of the
same quadratic Julia set, I could entwine two
arbitrary quadratic Julia sets. So I tried perturbing
f(
z). My first attempt,
 = \frac{z + a}{b(z^2 + 1)})
, did exactly that, and Matchmaker was born.
The original
f(
z) is a subfamily of Matchmaker obtained when
a = 0, and its Mandelbrot occurs as the
b-plane through the origin of the Matchmaker parameter space. The Mandelbrot images produced from other slices, even parallel ones, can be very interesting, as shown here.
In this image and in the first
Portal, both critical points are studied. In
Portal, black points have no attractors (the Julia set is the whole Riemann sphere). Grey/blue points have one attractor. Pink points have two. The gradients in the latter two areas map smoothed iterations, calculated for both critical points and then averaged (unless one critical point failed to converge to anything; then only the other's smoothed iterations value gets used).
In
Portal II, there are two more layers. One colors the points with no finite attractors; the critical points are iterated in tandem and their separations after each iteration are recorded and averaged. They can get quite far apart, since the numerator degree doesn't exceed the denominator degree and so infinity is not a special point on the Riemann sphere for this map.
The other additional layer brings out the filament structures visible in the one-attractor regions. These filament structures can include all the familiar Mandelbrot bestiary: seahorses, elephants, and so forth.
This filament structure results when the critical point that doesn't "own" the attractor wanders through the dynamic plane and sometimes hits the Julia set, and so has Misiurewicz points and other structures. Where this occurs, the difference between the two smoothed iteration values jumps as it's much higher for the critical point that's near the Julia set than it is for the one that's in the immediate basin of the attractor. So this difference is used to enhance the filament structure using a solid-white layer with an alpha channel that goes from transparent to opaque as the difference rises.
Near the filaments, typically one converges slowly (the one associated with the filaments and with a nearby other bud) and one converges quickly (the one associated with the bud we're in).
The filaments can also be made to contrast more, without an added layer, by weighting the average of the two critical points' smoothed iteration values; weighting 99% in favor of the one with more iterations, at each point, tends to do an okay job. Here, though, the difference-layer method is used.
Now some details about the structure of this Mandelbrot.
The outer grey "void" is actually the period-1 component. The Julia sets here are dusts, with nearly every point going to the sole attractor (which is not generally zero; in Matchmaker, zero goes to
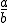
and therefore is not a fixed point for
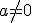
).
The large circular bud is period-2. In this and all higher-period components where there is just one attractor, the Julia set is connected: if the period is
n, consider the rational map made by composing Matchmaker with itself
n times, and note that the period-
n attractor of the original map must be
n attracting fixed points of this map, and their basin boundaries must coincide with one another and with the Julia set, which must be the Julia set of the original map. Hence that Julia set is connected and the attracting basin tiles the Riemann sphere with connected chunks of itself. The result is to take a quadratic Julia set and "extend" it and fold it in on itself to densely cover the entire Riemann sphere.
But the
really interesting stuff happens where two attractors coexist. At these parameter values, one gets arbitrary pairs of connected quadratic Julia sets that each have to fill the space outside the other, so they become fractally entwined in extravagantly complex and beautiful ways.
The downside is that long calculation times are inevitable with Matchmaker images. The Julia sets frequently require aggressive antialiasing to render decently, whereas the Mandelbrot images are plagued by large expanses of space within which there are no attractors in the dynamics, every point in which therefore has to be iterated to the max. And the max needs to be set high, at least a million, to get a decent component interior gradient. To add insult to injury, for the Mandelbrot images the calculation time gets a final doubling from iterating both critical points.
Numerous Mandelbrot and (especially) Julia images are forthcoming.
Eventually.


















