The All New FractalForums is now in Public Beta Testing! Visit FractalForums.org and check it out!
|
|
|
||||||
| Introducing the Kalibrot | ||||||
| Previous Image | Next Image | ||||||
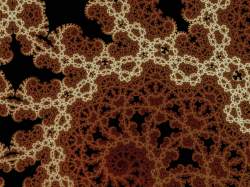
| Description: Want to add some texture to those low-iteration Mandelbrots? Kalibrot to the rescue! Kaliset patterns replace boring old iteration bands, seamless and brimming with detail.
Stats: Total Favorities: 0 View Who Favorited Filesize: 428.13kB Height: 900 Width: 1200 Discussion Topic: View Topic Keywords: Kali Mandelbrot Posted by: Pauldelbrot  July 15, 2011, 05:11:38 PM July 15, 2011, 05:11:38 PMRating: Has not been rated yet. Image Linking Codes
|
||||||
| 0 Members and 1 Guest are viewing this picture. |
|
Comments (2)  |
|
| Pauldelbrot | July 16, 2011, 12:58:06 AM Interesting. All not quite the same approach: mine is post-iteration and textures the "background", your top one seems to do N Mandelbrot iterations and then switch to Kaliset, and your bottom one seems similar to mine, but doesn't generate seamless patterns. Mine takes the partial smoothed iteration and the decomp angle and then folds them in a complex way. Because there is a period doubling between one iteration band and the next, I determined this structure was needed: Code: A-B-A-B-A but compressed, so the top and bottom edges end up applying to one decomp interval, the top edge at the top of the iteration band and the bottom edge at the bottom. Same-labeled points had to be identified. I ended up with this: x = atan2(z.r,z.i) // in -pi...pi y = [complicated ... 1 at bottom of iteration band and 0 at top] x = abs(x/pi) // fold left half of above diagram onto right half x = x * (1 + y) // stretch x at bottom of iteration band if (x > 1) x = 2 - x // fold rightmost large triangle over left edge if (x > y) { t = x; x = y; y = t} // fold square in center-right across diagonal if (x > (1 - y)) { t = 1 - x; x = 1 - y; y = t} // fold across other diagonal if (y > 0.5) y = 1 - y; // fold through the row of Cs The result is to fold all the tiny ABC triangles into one. So a triangular bit of the Kaliset can be tiled in a manner that will be seamless within the above diagram, and because of the period doubling, the top edge of that diagram for iteration N aligns with half the bottom edge for iteration N - 1 -- but that's okay, as everything matches up. Also the left and right edges end up straight, and matching, between decomp segments along the band. In fact, *any* continuous 2d function of xy could be used to color points and get a seamless pattern, including any 2d fractal image, but things like the kaliset that naturally contain mirror lines look better when kaleidoscopically folded (one triangle repeated over and over) like this. |
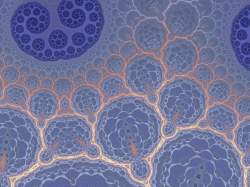
| Kali | July 15, 2011, 06:21:03 PM Nice... I've done something like that when testing the software that I'm (slowly) developing, wich will be based on 2D formula combinations. I posted the following images some time ago in my thread about the project: http://www.fractalforums.com/announcements-and-news/fractkali/45/ This is combined with Kaliset:   Also in this video I'm using a combination with patterns from another formula (A linear combination of Mandelbrot on real numbers) Another good idea could be the use of 2D formulas into 3D ones, for coloring or bump-maps of the surfaces. There's a recently Aexion post about adding textures and bump mapping to the Mandelbox, but with predefined drawings or textures. A 2D formula should work fine for that. Btw, thanks for using my formulas, you are doing very well  |
Powered by SMF Gallery Pro