|
gds-entropy
|
 |
« on: January 25, 2017, 11:30:04 PM » |
|
A technique which is my favorite, and I am not aware of its popularity, is the use of meta-formulae. These are fractal formulae that follow the convention of an original but at a much higher level. One such is below [and attached, and I copy the text of the Flickr description below as well]: https://www.flickr.com/photos/gds-entropy/31665738024/in/dateposted-public/I always share all of my formulae unless I have lost them and would need to reconstruct them from Fractal Explorer *.frs files. I'm both too busy and too lazy to do this, but will freely share the *.frs files; I would appreciate a link back to my Flickr if you use them and please share any derivative formulae with the world in return. <ot> For any of the cellular automata and PDE simulations on my Flickr, I cannot post code on that platform, they mangle it beyond imagination. I am always open to collaborations though, such as the one I undertook with Softology/Jason Rampe which resulted in us largely cracking the McCabe "Very Cellular Automata"...that was fun. Link.. https://softologyblog.wordpress.com/2016/11/17/more-experiments-with-coupled-cellular-automata/</ot> The Level 3 Meta-Mandel formula looks almost like a Mandeljulia, for certain values of Real. While this IS a Julia rendered formula colored according to Newton and Log(|Z|), it follows the rough pattern of the Mandelbrot fractal. This makes sense, even though it does so for only ONE particular value of real [-0.1], because the formula is itself a meta-Mandelbrot. Look at it. I simply followed the convention of z*z+c to three levels...so thing A times itself plus thing B. Thing B is simply an inverted thing A which follows the same convention. Level 0 is: z*z+c Level 1 is: ((z*z+c)*(z*z+c)+(c*c+z)) Level 2 is: (((z*z+c)*(z*z+c)+(c*c+z)) * ((z*z+c)*(z*z+c)+(c*c+z)) + ((c*c+z)*(c*c+z)+(z*z+c))) Level 3 is: ((((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))*(((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))+(((c*c+z)*(c*c+z)+(z*z+c))*((c*c+z)*(c*c+z)+(z*z+c))+((z*z+c)*(z*z+c)+(c*c+z)))) Try this technique yourself with other models, you will get interesting results! Ian |
|
|
|
 Logged
Logged
|
|
|
|
|
PieMan597
|
 |
« Reply #1 on: January 26, 2017, 12:18:03 AM » |
|
This is very cool!
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #2 on: January 26, 2017, 01:15:49 AM » |
|
There was a thread about this technique a while a go. Pretty neat indeed. I believe it was called Meta-brot at the time.
I wonder if there is some limit estimate one could do to this, so you get a "short" formula that approximates the limit and then works more like the original iteration formula.
Although the c²+z might be new? I don't know what the other thread had as a pattern.
|
|
|
|
« Last Edit: January 26, 2017, 01:33:57 AM by kram1032 »
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #3 on: January 26, 2017, 01:32:21 AM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
gds-entropy
|
 |
« Reply #4 on: January 26, 2017, 05:00:15 AM » |
|
Very interesting, and certainly some similarity in the output. If the formula I posted is rendered as a Mandelbrot, it produces a rather boring star shape though; the most interesting manifestations seem to be when treated as Julia. Ian |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Dinkydau
|
 |
« Reply #5 on: January 26, 2017, 09:36:31 AM » |
|
This is amazing.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
SamTiba
|
 |
« Reply #6 on: January 26, 2017, 10:18:05 AM » |
|
expanded Formula for the pattern level 3 with c = -0.1:
z^16 + -0.8*z^14 + 4*z^13 + 0.32*z^12 + -2.4*z^11 + 9.92*z^10 + 0.76*z^9 + -4.1862*z^8 + 11.856*z^7 + 0.95832*z^6 + -2.782*z^5 + 13.888144*z^4 + 0.51864*z^3 + -1.191008*z^2 + 0.984064*z^1 + 0.03988026
I computed it not using the diverging method and it looks rather like a normal Julia-set with nothing special.
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #7 on: January 26, 2017, 12:48:33 PM » |
|
It's beautiful though. I still wonder what my own works would eventually actually look like. I need to make an iterative density plot version of it somehow. - In my old mathematica code I just evaluated all the points without ever actually plotting the result mid-calculation to see how it progresses. If anybody has a take on it, that would be nice. Also, is there a similar, what appears to be a closed form, for this variant of the Metabrot compared to the other? Just to reiterate, here is the Mathematica code that recursively builds all points in the set given a specific value for c and up to a specific recursion depth n: z[0, _, _] := 0
z[n_, c_, -1] := {1/2 (1 - Sqrt[1 - 4 z[n - 1, c, -1]]) + c,
1/2 (1 + Sqrt[1 - 4 z[n - 1, c, -1]]) + c}
z[n_, c_, 1] := {1/2 (1 - Sqrt[1 - 4 z[n - 1, c, 1]]) + c,
1/2 (1 + Sqrt[1 - 4 z[n - 1, c, 1]]) + c}
z[n_, c_] := {z[n, c, -1], z[n, c, 1]} Yesterday I coded up what should be the equivalent function in Python: import collections
from cmath import sqrt
def flatten(l):
for el in l:
if isinstance(el, collections.Iterable) and not isinstance(el, (str, bytes)):
yield from flatten(el)
else:
yield el
def z(n, c, b=None):
if n == 0:
yield 0
elif b == -1:
for _z in flatten(z(n-1, c, -1)):
yield .5 * (1 - sqrt(1 - 4 * _z)) + c
yield .5 * (1 + sqrt(1 - 4 * _z)) + c
elif b == 1:
for _z in flatten(z(n - 1, c, 1)):
yield .5 * (1 - sqrt(1 - 4 * _z)) + c
yield .5 * (1 + sqrt(1 - 4 * _z)) + c
elif b is None:
yield flatten(z(n, c, -1))
yield flatten(z(n, c, 1))
So what has to be done with this code is to evaluate it with all possible values for c: That would then be the actual Meta-Mandelbrot Set. For any specific value of c, it's the Meta-Julia-set. To find my potential closed form expression, I simply kept expanding larger and larger meta-iterations of the M-set as given at the start of the other thread, and I observed that the first few polynomial coefficients remained constant; the polynomial family converged to a limit which appears to be the expansion of ) which is one of two inverses of 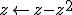 , the other one being ) . These two formulae are what the above functions iterate over. It was relatively easy due to c not being involved in the iteration though. This new take also involves powers of c and thus it will be quite a bit tougher, I assume. Though perhaps it's just as simple to do. Gotta expand a bunch of terms and see if any pattern emerges. |
|
|
|
« Last Edit: January 26, 2017, 12:55:15 PM by kram1032 »
|
 Logged
Logged
|
|
|
|
|
Chillheimer
|
 |
« Reply #8 on: January 26, 2017, 04:34:11 PM » |
|
uhhh fascinating!!  thanks for sharing. |
|
|
|
|
 Logged
Logged
|
--- Fractals - add some Chaos to your life and put the world in order. ---
|
|
|
|
SamTiba
|
 |
« Reply #9 on: January 27, 2017, 12:58:18 AM » |
|
I am somehow worrying about the small dots where the number of iterations get higher not beeing on the spiral-sequence.
Can you zoom in there, gds-entropy?
Or can someone confirm them or could it also be a bug?
I thought of finding nice known patterns for formulas aswell, already tried some things like for example the legendre polynoms.
They have special behaviours but nothing extraordinary yet. There are also some nice continous fractions I would like to try out, hopefully the result is stunning.
If anyone has ideas feel free to share!
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
gds-entropy
|
 |
« Reply #10 on: January 27, 2017, 08:55:04 PM » |
|
I am somehow worrying about the small dots where the number of iterations get higher not beeing on the spiral-sequence.
Can you zoom in there, gds-entropy?
Or can someone confirm them or could it also be a bug?
Without having the source of Fractal Explorer I cannot really say if it is a bug or not. They no longer respond to their old e-mail at the Ukrainian government...anyone know how to contact them? I am trying to track them both down with LinkedIn and using academic routes. I wish I had bought a license to it when I had the chance in 2005. In FE I am using 8192 iterations, N-Set Method, View As Julia, Log Counting |Z|-area, and Linear(Ident) within color control. The [inside and outside] dots remain regardless of the settings I choose, with only a few exceptions that look like pure chaos so I couldn't tell the difference. They remain if I select Inverted too, albeit in a different place. It may be a Fractal Explorer thing, maybe not; it does not manifest in UF when just calculating the raw fractal, it is just black inside. However the image generated by SamTiba has [outside] dots, though I cannot say their relation to the ones in my image, as I have no context. The outside dots are tiny, complete copies of the fractal as a whole, rotated. I'll render one and upload it. I'm not sure how useful that information is. rsidwell from the UF forum was kind enough to make a UFM for me, in order to assist in migrating my formulae from FE to UF...those programs are so different... Honestly I much prefer FE for ease of use and all of the built in options...but alas, that infernal 16bit Formula Compiler fails to function without a 16 bit subsystem being in the newer windows...[I will try both XP Mode in win7 and a VM...]. With UF I'm essentially going to have to reverse engineer all of the modes that FE had...ugh...that is a lot of reimplementation work for what is essentially a solved problem. Here is the UFM: Ian1-M {
;
; Ian McDonald custom formula from the forum (Mandelbrot mode)
;
init:
z = (0,0)
c = #pixel
loop:
z = ((((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))*(((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))+(((c*c+z)*(c*c+z)+(z*z+c))*((c*c+z)*(c*c+z)+(z*z+c))+((z*z+c)*(z*z+c)+(c*c+z))))
bailout:
|z| <= @bailout
default:
title = "Ian1 Mandelbrot"
float param bailout
caption = "Bailout value"
default = 4.0
endparam
switch:
type = "Ian1-J"
seed = #pixel
bailout = bailout
}
Ian1-J {
;
; Ian McDonald custom formula from the forum (Julia mode)
;
init:
z = #pixel
c = @seed
loop:
z = ((((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))*(((z*z+c)*(z*z+c)+(c*c+z))*((z*z+c)*(z*z+c)+(c*c+z))+((c*c+z)*(c*c+z)+(z*z+c)))+(((c*c+z)*(c*c+z)+(z*z+c))*((c*c+z)*(c*c+z)+(z*z+c))+((z*z+c)*(z*z+c)+(c*c+z))))
bailout:
|z| <= @bailout
default:
title = "Ian1 Julia"
param seed
caption = "Seed"
default = (-0.1, 0)
endparam
float param bailout
caption = "Bailout value"
default = 4.0
endparam
switch:
type = "Ian1-M"
bailout = bailout
} |
|
|
|
« Last Edit: January 27, 2017, 09:01:08 PM by gds-entropy, Reason: added info »
|
 Logged
Logged
|
|
|
|
|
3dickulus
|
 |
« Reply #11 on: January 28, 2017, 06:29:24 AM » |
|
this looks really interesting and a bit familiar, like something I found while investigating BioMorphs using Fragmentarium, I tried your level 3 with the standard Mandelbrot.frag using this to calculate z... (i think I got it right?) and in the spirit of the OP I thought I would share what I have too  for (i = 0; i < Iterations; i++) {
z = (
cMul(
(
cMul((cMul((cMul(z,z)+c),(cMul(z,z)+c))+(cMul(c,c)+z)),
(cMul((cMul(z,z)+c),(cMul(z,z)+c))+(cMul(c,c)+z)))+
(cMul((cMul(c,c)+z),(cMul(c,c)+z))+(cMul(z,z)+c))
),
(
cMul((cMul((cMul(z,z)+c),(cMul(z,z)+c))+(cMul(c,c)+z)),
(cMul((cMul(z,z)+c),(cMul(z,z)+c))+(cMul(c,c)+z)))+
(cMul((cMul(c,c)+z),(cMul(c,c)+z))+(cMul(z,z)+c))
)
)+
(
cMul((cMul((cMul(c,c)+z),(cMul(c,c)+z))+(cMul(z,z)+c)),
(cMul((cMul(c,c)+z),(cMul(c,c)+z))+(cMul(z,z)+c)))+
(cMul((cMul(z,z)+c),(cMul(z,z)+c))+(cMul(c,c)+z))
)
);
if (dot(z,z)> 100.0) break;
}
...c.x = -0.1077844 c.y = 0.0000000 image meta1.png which looks similar to the biomorph plot of z=z+z²+c Power = 4;
vec2 Plot(vec2 a) {
vec2 b;
b.x = sqrt (a.x * a.x + a.y * a.y);
b.y = atan (a.y / a.x);
if ( a.x < 0.) b.y += 3.141592;
b.x = pow(b.x,float(Power));
b.y *= float(Power);
a.x = cos(b.y) * b.x;
a.y = sin(b.y) * b.x;
return a;
}
...
for (i = 0; i < Iterations; i++) {
z += Plot(z) + c;
if (dot(z,z)> 100.0) break;
}
...
...c.x=0.0416913 c.y=0.0000000 meta2.png both of these images are at about 40 iterations |
|
|
|
 Logged
Logged
|
|
|
|
|
gds-entropy
|
 |
« Reply #12 on: January 31, 2017, 12:49:34 AM » |
|
I am somehow worrying about the small dots where the number of iterations get higher not beeing on the spiral-sequence.
Can you zoom in there, gds-entropy?
Here is the fractal found at: [which is one of the dots in the halo] x: -0.589605376476377944 y: 0.162209338090551179 This is just to the upper left of the leftmost set of spirals. https://www.flickr.com/photos/gds-entropy/31769659574/in/dateposted-public/ |
|
|
|
 Logged
Logged
|
|
|
|
|
gds-entropy
|
 |
« Reply #13 on: January 31, 2017, 12:56:34 AM » |
|
this looks really interesting and a bit familiar, like something I found while investigating BioMorphs using Fragmentarium, I tried your level 3 with the standard Mandelbrot.frag using this to calculate z... (i think I got it right?) and in the spirit of the OP I thought I would share what I have too  Thank you for sharing.  The first image is the closest I have seen yet, it is structurally identical from what I can tell. Other interesting forms are at Real -0.2 and -0.1. Here is the one for R-0.2: https://www.flickr.com/photos/gds-entropy/32052371270/in/dateposted-public/ |
|
|
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #14 on: January 31, 2017, 08:58:01 AM » |
|
It reminds me the Spider fractint formula. Also I wonder what happens when you expand the massive product  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|


















