END OF AN ERA, FRACTALFORUMS.COM IS CONTINUED ON FRACTALFORUMS.ORG

Do power 3 mandelbrot have something simmilar? I hadn't seem some good zooms of power 3 mbrot with named valleys, structures and so on. But are there something simmilar in power 3 mandelbrot?

In higher powers features seems to dissapear, but in power 3 in deeper zooms there could be some interesting structures with different simmetries than these.

For some reason in mandelbrot sets with a power higher than 2, when zooming, minibrots approach much quicker and the details are much more stacked together around the minibrots. The mandelbrot set with power 2 allows for much longer zooms before reaching a minibrot. You can go much further into the middle of something with new overwhelming details appearing all the time, without having to change direction, which makes it the most suitable for zooms in my opinion. It make some kind of build-up chaoticness that becomes more extreme over time. You can see how slowly the details show up with a power of 50 in this video. Minibrots are constantly visible. Compare this the zoomin into the antenne of the power 2 mandelbrot set.
<a href="http://www.youtube.com/v/c_Xsd7jTQcg&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/c_Xsd7jTQcg&rel=1&fs=1&hd=1</a>

Further to the above, the change in behavior is because the period-"doubling" divides ln(z - P) by the power n from zⁿ + c, where P is the center of the minibrot. That makes angular features repeat n times, so with the quadratic M-set they double, then double again, etc. approaching the minibrot, but in z³ they triple, then triple again, and etc. Meanwhile, the logarithm of magnification shrinks similarly: depth to first doubling in quadratic is halved to get further depth to second doubling. With the cubic M-set it's reduced to 1/3.

The actual depth of the minibrot can be calculated from the depth of the final eccentric zoom by noting that the above is a geometric series with ratio 1/n, which converges on



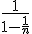
which is, as plynch27 said, n/(n - 1).

So if the last eccentric zoom is at some depth, the further depth to the minibrot is equal to that for z², only half that for z³, a third for z⁴, and so forth.

Put another way, if you want the section from the final off-center zoom to the minibrot to have a given length, the length of the zoom to that off-center zoom has to be larger by a factor of n - 1. In other words by how many lobes the minibrot has! The two-lobed z³ requires double, for example. So if you want the zoom from doubling on to be a factor of 10⁵⁰ you need to go off-center from time to time all the way down to 10¹⁰⁰. With three-lobed z⁴ it would have to be 10¹⁵⁰. And so forth.

This makes getting those lengthy zooms to minibrots much slower with higher powers, too, because compute time contributed by multiplies goes up quadratically with log mag and the number of multiplies per iteration goes up as log power -- for example, z⁸ requires three successive squarings. So if you want the final segment from last off-center zoom to minibrot to be of a fixed length, the time needed for the whole zoom sequence scales as n(log₂ n)². The first few such numbers, divided by that for n = 2, are:

n		time
2		1
3		3.768159193038392
4		8
5		13.478375194568137
6		20.04609339040372
7		27.584345804403696
8		36
9		45.2179103164607
10		55.176031338009906
11		65.8221691821511
12		77.11173678946133

It's growing slower than quadratic, but substantially faster than linear. In reality it's not quite as tidy; the actual number of multiplies is never fractional, so the log₂ ceiling should really be taken, which gives this corrected table:

n		time
2		1
3		6
4		8
5		22.5
6		27
7		31.5
8		36
9		72
10		80
11		88
12		96

For z¹², this predicts a nearly 100-fold slowdown for a fixed depth from final off-center zoom to minibrot compared to for the plain Mandelbrot set, with a 12-times deeper zoom overall.

So, basically what everyone else said, but putting concrete numbers to "minibrots approach much quicker".

you made it to orbittrap
http://orbittrap.ca/?p=4358

lols, although i never got a response from him, he seems to read my mails
i was upset of the classification of most of the images

Now I see what took so long.

Thanks!