|
twinbee
|
 |
« Reply #15 on: November 25, 2009, 11:44:58 AM » |
|
Hi kram1032, I corrected the file names.
Buddhi, that's fantastic - looks so wooden and complex. Kind of structure/texture that could easily in the real world.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #16 on: November 25, 2009, 10:01:47 PM » |
|
ah, nice twinbee  Buddhi: Now I wonder about a castle-version of your Menger sphere  Also twinbee: What about both a multiperspective (say, three points of infinity (PoI) for three axes) or an inverse perspective (PoI lies on the image plane) or maybe a "central" perspective (PoI in the center of the Menger-sponge...) Afaik, a lot of paintings used that. The PoI is the point, where all infinite straight lines meet due to perspective distortion. Could give interesting twists on the shape  Or, also possible maybe, what's about an hyperbolic Menger-sponge, where rather than 27 cubes form a bigger cube, say 84 do so... - I'm not sure right now how that looks like but my idea is, that more cubes can touch in hyperbolic space while still tesselating the plane. basically you could do the same as in euclidean, but instead of letting 1 corner of a cube letting touch 6 other cubes' corners, you could change that to a higher number... (probably, though, the 2D-case should be done first, before investigating in the 3D-case...) Oh, and something probably way simpler: Could you please upload pngs or something? especially the colourful castle suffers a lot from the jpeg-compression  |
|
|
|
« Last Edit: November 25, 2009, 10:03:46 PM by kram1032 »
|
 Logged
Logged
|
|
|
|
|
|
|
jehovajah
|
 |
« Reply #18 on: November 26, 2009, 02:26:23 AM » |
|
could rf used as a visualisation of structured space say in a crystal lattice, or a planetary/ gravitational / molecular system.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
|
|
twinbee
|
 |
« Reply #20 on: January 04, 2010, 04:59:13 PM » |
|
I don't know. I leave the Mandelbulb alone for 5 minutes, and look what it's gone and done to my precious Menger sponge!!  Big 2500x2500 version available here:  For the curious, this is a simple boolean "AND" to the Menger sponge and Mandelbulb. In other words, each point has to be part of both sets for it to be part of the new hybrid set. *****EDIT***** kram1032, those perspective tricks sound good, and probably not too tricky to implement (I've sometimes thought about inverse perspective). I'll see what I can do. Here's a full PNG of the earlier castle menger sponge btw: http://www.skytopia.com/project/fractal/new/menger-persp2b.png |
|
|
|
« Last Edit: January 04, 2010, 05:37:53 PM by twinbee »
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #21 on: January 04, 2010, 05:40:59 PM » |
|
Fantastic idea and render!!! I think it is impossible to render this with DE :-)
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #22 on: January 04, 2010, 06:49:14 PM » |
|
heh... nice half-molten Menger  It had some thermite for dinner, right? Already curious about twisted perspectives  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #23 on: September 17, 2010, 09:28:14 PM » |
|
Sorry for bumping this old thread. I'm working on aperiodic tilings thanks to tomkh's thread and just think it's related to this dicussion. My objective is to find DE estimate for aperiodic 3D tilings. On the way I remembred this thread and am having answers to a some questions: Here are the DE for twinbee's Menger sponge and Buddhi's sphere sponge: //Derived from twinbee's algorithm
MengerSponge3(x, y, z) {//by recursively digging a box
x=x*0.5+0.5;y=y*0.5+0.5;z=z*0.5+0.5;//center it by changing position and scale
xx=abs(x-0.5)-0.5;yy=abs(y-0.5)-0.5;zz=abs(z-0.5)-0.5;
d1=max(xx,max(yy,zz));//distance to the box
d=d1;//current computed distance
p=1;
for(m=1; m<MI ; m++) {
xa = 3*x*p % 3;
ya = 3*y*p % 3;
za = 3*z*p % 3;
p*=3;
//we can also translate/rotate (xa,ya,za) without affecting the DE estimate
xx=0.5-abs(xa-1.5);yy=0.5-abs(ya-1.5);zz=0.5-abs(za-1.5);
d1=min(max(xx,zz),min(max(xx,yy),max(yy,zz)))/p;//distance inside the 3 axis aligned square tubes
d=max(d,d1);//intersection
}
return d*2; //the distance estimate. The "*2" is because of the scaling we did at the begining of the function
} //derived from Buddhi's algorithm
SphereSponge3(x, y, z) {//by recursively digging space
//Same as for the Menger sponge but with spheres
x+=1;y+=1;z+=1;
intrad=param1;
scl=3;mod=4;
a=x;b=y;c=z;k=2;
d=-100;
for (L = 0; L < MI ; L++)
{
xx = a * k % mod - 0.5*mod;
yy = b * k % mod - 0.5*mod;
zz = c * k % mod - 0.5*mod;
r2=xx*xx + yy*yy + zz*zz;
d1=(intrad-sqrt(r2))/k;//distance to the edge of the sphere (positive inside)
d=max(d,d1);//intersect
k *= scl;
}
return d;// distance estimate
} (needs some optimizations  but it is already quite fast  ) It's possible to use the same technique to other figures (fractals and tilings). Fantastic idea and render!!! I think it is impossible to render this with DE :-)
It's actually possible (and well known): the intersection is obtained by taking the maximum DE of the two objects. That's what I am using in the codes above. union can also be obtained by taking the minimum DE instead. BTW: There is another well known trick In distance fied rendering: Blending. Just take a linear (or higher order) interpolation of the DE of the two objects. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #25 on: October 09, 2013, 05:41:39 PM » |
|
Found an error in the Fragmentarium implement of NewMenger.  The DE is buggy currently; the sponge tends to disappear.  If you replace... float DE(vec3 p)
{
p=p*0.5+vec3(0.5);
vec3 pp= abs(p-0.5)-0.5;
float k=1.0;
float d1 = max(pp.x,max(pp.y,pp.z));
float d=d1;
for (int i = 0; i < Iterations ; i++)
{
vec3 pa = mod(3.0*p*k, 3.0);
k *= Scale;
pp = 0.5-abs(pa-1.5)+Offset;
pp*=rot;
d1=min(max(pp.x,pp.z),min(max(pp.x,pp.y),max(pp.y,pp.z)))/k;//distance inside the 3 axis aligned square tubes
d=max(d,d1);
if (i<ColorIterations) orbitTrap = min(orbitTrap, abs(vec4(pp,dot(pp,pp))));
}
// Use this to crop to a sphere:
// float e = clamp(length(z)-2.0, 0.0,100.0);
// return max(d,e);// distance estimate
return d;
} with... float DE(vec3 p)
{
p=p*0.5+vec3(0.5);
vec3 pp= abs(p-0.5)-0.5;
float k=1.0;
float d1 = max(pp.x,max(pp.y,pp.z));
float d=d1;
for (int i = 0; i < Iterations ; i++)
{
vec3 pa = mod(3.0*p*k, 3.0);
pp = 0.5-abs(pa-1.5)+Offset;
pp*=rot;
d1= (1/k) * min(max(pp.x,pp.z),min(max(pp.x,pp.y),max(pp.y,pp.z)))/k;//distance inside the 3 axis aligned square tubes
d=max(d,d1); k *= Scale;
if (i<ColorIterations) orbitTrap = min(orbitTrap, abs(vec4(pp,dot(pp,pp))));
}
// Use this to crop to a sphere:
// float e = clamp(length(z)-2.0, 0.0,100.0);
// return max(d,e);// distance estimate
return d;
} Because d1 must be properly scaled (multiplied by 1/k). Now it renders perfectly!    |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
Syntopia
|
 |
« Reply #26 on: October 13, 2013, 11:46:24 PM » |
|
Hi DarkBeam,
The code you posted produce much worse results than the original code on my computer. Are you sure you didn't change something else? Can you post the full fragment?
|
|
|
|
|
 Logged
Logged
|
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #27 on: October 15, 2013, 12:43:58 PM » |
|
 me = stuuuupid!!!!!!!! d1= (1/k) * min(max(pp.x,pp.z),min(max(pp.x,pp.y),max(pp.y,pp.z))) /k;//distance inside the 3 axis aligned square tubes Is of course wrong because I divided twice! It should be d1= (1/k) * min(max(pp.x,pp.z),min(max(pp.x,pp.y),max(pp.y,pp.z)));//distance inside the 3 axis aligned square tubes sorry but as weird as it sounds; I can not say if it's correct or send the script because my drivers fail to run now  - btw it works great into Mandelbulb3D 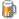
|
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|


















