Hello,
Here are some renderings of a class of fractals which I call "Kaleidoscopic IFS". There is a big variations of shapes one can get with this method.
I began with this algorithm to get DE for symmetric Sierpinski tetrahedron:
//scale=2
//bailout=1000
sierpinski3(x,y,z){
r=x*x+y*y+z*z;
for(i=0;i<10 && r<bailout;i++){
//Folding... These are some of the symmetry planes of the tetrahedron
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
if(y+z<0){y1=-z;z=-y;y=y1;}
//Stretche about the point [1,1,1]*(scale-1)/scale; The "(scale-1)/scale" is here in order to keep the size of the fractal constant wrt scale
x=scale*x-(scale-1);//equivalent to: x=scale*(x-cx); where cx=(scale-1)/scale;
y=scale*y-(scale-1);
z=scale*z-(scale-1);
r=x*x+y*y+z*z;
}
return (sqrt(r)-2)*scale^(-i);//the estimated distance
}
Then I added a rotation before the fold or before the stretch or both.
//scale=2
//bailout=1000
sierpinski3(x,y,z){
r=x*x+y*y+z*z;
for(i=0;i<10 && r<bailout;i++){
rotate1(x,y,z);
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
if(y+z<0){y1=-z;z=-y;y=y1;}
rotate2(x,y,z);
x=scale*x-(scale-1);
y=scale*y-(scale-1);
z=scale*z-(scale-1);
r=x*x+y*y+z*z;
}
return (sqrt(r)-2)*scale^(-i);//the estimated distance
}
Then I allowed the center of stretching to be modified.
//scale=2
//bailout=1000
sierpinski3(x,y,z){
r=x*x+y*y+z*z;
for(i=0;i<10 && r<bailout;i++){
rotate1(x,y,z);
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
if(y+z<0){y1=-z;z=-y;y=y1;}
rotate2(x,y,z);
x=scale*x-CX*(scale-1);
y=scale*y-CY*(scale-1);
z=scale*z-CZ*(scale-1);
r=x*x+y*y+z*z;
}
return (sqrt(r)-2)*scale^(-i);//the estimated distance
}
(In my implementation [CX,CY,CZ] is constrained to be on the unit sphere)
This gives 1+3+3+2=9 parameters in total (scale->1,rotation1->3,rotation2->3,center of stretch->2).
The set of folding operation may be different. Here are those that I've tried:
- half tetrahedral symmetry planes: the same than above.
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
if(y+z<0){y1=-z;z=-y;y=y1;}
- 2nd half tetrahedral symmetry planes:
if(x-y<0){x1=y;y=x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(y-z<0){y1=z;z=y;y=y1;}
- full tetrahedral symmetry planes:
if(x-y<0){x1=y;y=x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(y-z<0){y1=z;z=y;y=y1;}
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
if(y+z<0){y1=-z;z=-y;y=y1;}
- cubic symmetry planes:
x=abs(x);y=abs(y);z=abs(z);
- half octahedral symmetry planes:
if(x-y<0){x1=y;y=x;x=x1;}
if(x+y<0){x1=-y;y=-x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(x+z<0){x1=-z;z=-x;x=x1;}
- full octahedral symmetry planes:
x=abs(x);y=abs(y);z=abs(z);
if(x-y<0){x1=y;y=x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(y-z<0){y1=z;z=y;y=y1;}
Ah! I forgot the pictures

:
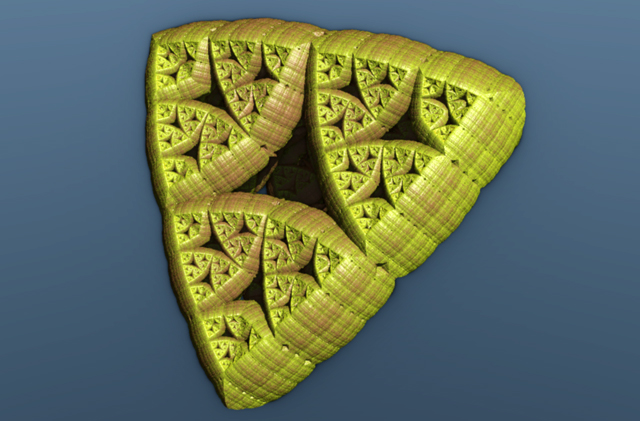

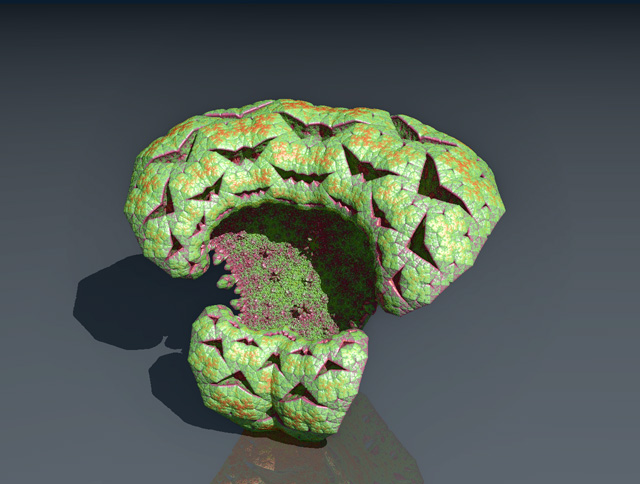
se also:
http://www.fractalforums.com/index.php?action=gallery;su=user;cat=164;u=932
The last picture is done with this algorithm:
Menger3(x,y,z){
r=x*x+y*y+z*z;
for(i=0;i<MI && r<bailout;i++){
rotate1(x,y,z);
x=abs(x);y=abs(y);z=abs(z);
if(x-y<0){x1=y;y=x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(y-z<0){y1=z;z=y;y=y1;}
rotate2(x,y,z);
x=scale*x-CX*(scale-1);
y=scale*y-CY*(scale-1);
z=scale*z;
if(z>0.5*CZ*(scale-1)) z-=CZ*(scale-1);
r=x*x+y*y+z*z;
}
return (sqrt(x*x+y*y+z*z)-2)*scale^(-i);
}
Which gives the menger sponge when used with CX=CY=CZ=1, scale=3 and no rotation.
___________________________________________
Here is another version of the menger Sponge (that makes it a true "Kaleidoscopic IFS"):
Menger3(x,y,z){
r=x*x+y*y+z*z;
for(i=0;i<MI && r<bailout;i++){
rotate1(x,y,z);
x=abs(x);y=abs(y);z=abs(z);
if(x-y<0){x1=y;y=x;x=x1;}
if(x-z<0){x1=z;z=x;x=x1;}
if(y-z<0){y1=z;z=y;y=y1;}
z-=0.5*CZ*(scale-1)/scale;
z=-abs(-z);
z+=0.5*CZ*(scale-1)/scale;
rotate2(x,y,z);
x=scale*x-CX*(scale-1);
y=scale*y-CY*(scale-1);
z=scale*z;
r=x*x+y*y+z*z;
}
return sqrt(x*x+y*y+z*z)*scale^(-i);
}


















