|
kram1032
|
 |
« Reply #105 on: May 20, 2010, 12:00:44 PM » |
|
Softology: I love how this one turns inside out and is nearly 2D in between  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Syntopia
|
 |
« Reply #106 on: May 20, 2010, 02:50:39 PM » |
|
Knighty, the number of reflections depend on the chosen symmetry planes and the order they are applied in. Using the set given by Jos Leys I had to repeat five times, for a total of 15 reflections, before scaling. I've optimized it a bit by including the x,y,z planes for the following 6 reflections:
int n = 0;
while (n < maxIterations) {
p.y = abs(p.y);
p.z = abs(p.z);
if (dot(p, n2)>0.0) { p *= n2Mat; }
p.x = abs(p.x);
p.z = abs(p.z);
if (dot(p, n1)>0.0) { p *= n1Mat; }
p = p*scale - offset*(scale-1.0);
if (dot(p,p)> bailoutSquared) break;
n++;
}
return (length(p) ) * pow(scale, -float(n));
And I think better solutions exist. Jos, when you said the icosa needed five folds, did you mean 5*3 reflections or just 5 reflections in total? And Softology, you asked for code. I think you can use the DE above together with these definitions: phi = 1.61803399; // golden ratio.
scale = 2.0;
offset = normalize(float3(1.0,phi-1.0,0.0));
n1 = normalize(float3(-phi,phi-1.0,1.0));
n2 = normalize(float3(1.0,-phi,phi+1.0));
n1Mat = reflectionMatrix(n1);
n2Mat = reflectionMatrix(n2);
// Return reflection matrix for plane with normal 'n'
float3x3 reflectionMatrix(float3 n)
{
return float3x3( 1.0 - 2.0*n.x*n.x, - 2.0*n.y*n.x , - 2.0*n.z*n.x,
- 2.0*n.x*n.y, 1.0 - 2.0*n.y*n.y , - 2.0*n.z*n.y,
- 2.0*n.x*n.z, - 2.0*n.y*n.z , 1.0 - 2.0*n.z*n.z );
}
|
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #107 on: May 20, 2010, 09:55:30 PM » |
|
Knighty, the number of reflections depend on the chosen symmetry planes and the order they are applied in. Using the set given by Jos Leys I had to repeat five times, for a total of 15 reflections, before scaling.
Yes it depends on the symmetry set choosen. If I'm not mistaken, 15 is the total number of symmetry planes of the dodeca and icosa. If you want only the icosa, 5 folds are sufficient. Same thing with the dodeca. The set that gives dodeca that way, is not the same for icosa. I've already found a "full" folding planes set for dodeca, icosa and the semi regular polyhedra that are in between. The number of folds was 9 but I think that it is possible with 8 folds. I've optimized it a bit by including the x,y,z planes for the following 6 reflections:
int n = 0;
while (n < maxIterations) {
p.y = abs(p.y);
p.z = abs(p.z);
if (dot(p, n2)>0.0) { p *= n2Mat; }
p.x = abs(p.x);
p.z = abs(p.z);
if (dot(p, n1)>0.0) { p *= n1Mat; }
p = p*scale - offset*(scale-1.0);
if (dot(p,p)> bailoutSquared) break;
n++;
}
return (length(p) ) * pow(scale, -float(n));
Whi do you use a symmetry matrix? Why not: float t=dot(p,n);
if (t>0.0) p-=2.0*t*n;
Which gives the same result and is, in principle, faster.  B.T.W, You are getting very nice results. Can anyone assist with the icos and dodec folding code? I cannot follow the snippets so far.
Jason.
Here is another variant that gives the "full" symmetry: #define PHI (0.5*(1+sqrt(5))) // Phi is the golden ratio
The three points that are the vertices of a fundamental triangle.
static ftris[3]={PHI,1,0};// vertex
static ftria[3]={PHI,0,0};// middle of edge
static ftric[3]={1/3*(1+2*PHI),0,PHI/3};//center of an icosa triangle.
#define IN3 (1/sqrt(14+6*sqrt(5))) //This is the normalisation factor of the following vector
static n3[3]={IN3*PHI,-IN3*(PHI^2),-IN3*(2*PHI+1)};//this is the normal of one of the folding planes.
// The 2 others planes' normals are: {0,1,0} and {0,0,1}
//
fractal(x,y,z,scale,rot[3][3]){
r=x*x+y*y+z*z;
for(i=0;i<MI && r<bailout;i++){
// PRE_ROTATE
x1=rot[0][0]*x+rot[1][0]*y+rot[2][0]*z;
y1=rot[0][1]*x+rot[1][1]*y+rot[2][1]*z;
z1=rot[0][2]*x+rot[1][2]*y+rot[2][2]*z;
x=x1;y=y1;z=z1;
// Foldings. 10 in total but 7 of them are abs() ;o)
x=abs(x);
y=abs(y);
z=abs(z);
t=x*n3[0]+y*n3[1]+z*n3[2];
if(t<0){x-=2*t*n3[0];y-=2*t*n3[1];z-=2*t*n3[2];}
y=abs(y);
z=abs(z);
t=x*n3[0]+y*n3[1]+z*n3[2];
if(t<0){x-=2*t*n3[0];y-=2*t*n3[1];z-=2*t*n3[2];}
y=abs(y);
z=abs(z);
t=x*n3[0]+y*n3[1]+z*n3[2];
if(t<0){x-=2*t*n3[0];y-=2*t*n3[1];z-=2*t*n3[2];}
// Stretching:
// for an icosahedron: stc[]=ftris[];
// for a dodecahedron: stc[]=ftric[];
// In general you can choose: stc[]=a*ftris[]+b*ftria[]+c*ftric[]; where: a+b+c=1;
x=scale*x-stc[0]*(scale-1);
y=scale*y-stc[1]*(scale-1);
z=scale*z-stc[2]*(scale-1);
r=x*x+y*y+z*z;
}
return (sqrt(x*x+y*y+z*z)-2)*(scale)^(-i);
}
Note the: if (t<0)... Syntopia and Jos Leys are doing: if (t>0)... This is because of the direction of the planes we are using! Perhaps that's why you were confused. (I was at some point  ) |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Syntopia
|
 |
« Reply #108 on: May 20, 2010, 11:08:10 PM » |
|
Yes it depends on the symmetry set choosen. If I'm not mistaken, 15 is the total number of symmetry planes of the dodeca and icosa. If you want only the icosa, 5 folds are sufficient. Same thing with the dodeca. The set that gives dodeca that way, is not the same for icosa. I've already found a "full" folding planes set for dodeca, icosa and the semi regular polyhedra that are in between. The number of folds was 9 but I think that it is possible with 8 folds.
I guess I'm a bit confused about what exactly count as a 'fold'. Do you mean you need only apply 5 conditional reflections before the scaling? Because I've only found (different) solutions with 6 conditional reflections for the icosa and dodeca. Whi do you use a symmetry matrix? Why not: float t=dot(p,n);
if (t>0.0) p-=2.0*t*n;
Which gives the same result and is, in principle, faster.  Well, both for readability, and because I assumed that matrix multiplications would be faster on the GPU. I just tested it, and I was wrong though: I get 22.8 fps (matrix) versus 23.4 fps (vector).  Best, Mikael. |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #109 on: May 20, 2010, 11:27:33 PM » |
|
Yes it depends on the symmetry set choosen. If I'm not mistaken, 15 is the total number of symmetry planes of the dodeca and icosa. If you want only the icosa, 5 folds are sufficient. Same thing with the dodeca. The set that gives dodeca that way, is not the same for icosa. I've already found a "full" folding planes set for dodeca, icosa and the semi regular polyhedra that are in between. The number of folds was 9 but I think that it is possible with 8 folds.
I guess I'm a bit confused about what exactly count as a 'fold'. Do you mean you need only apply 5 conditional reflections before the scaling? Because I've only found (different) solutions with 6 conditional reflections for the icosa and dodeca. Yes, by "fold", I mean "conditional reflexion". Sorry! that was 6 for me too. According to Jos Leys 5 are sufficient if I undestood well. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Softology
|
 |
« Reply #110 on: May 21, 2010, 02:15:10 AM » |
|
Thanks for the code snippets guys. That cleared everything up and I now have icosahedral and dodecahedral folding working. Jason 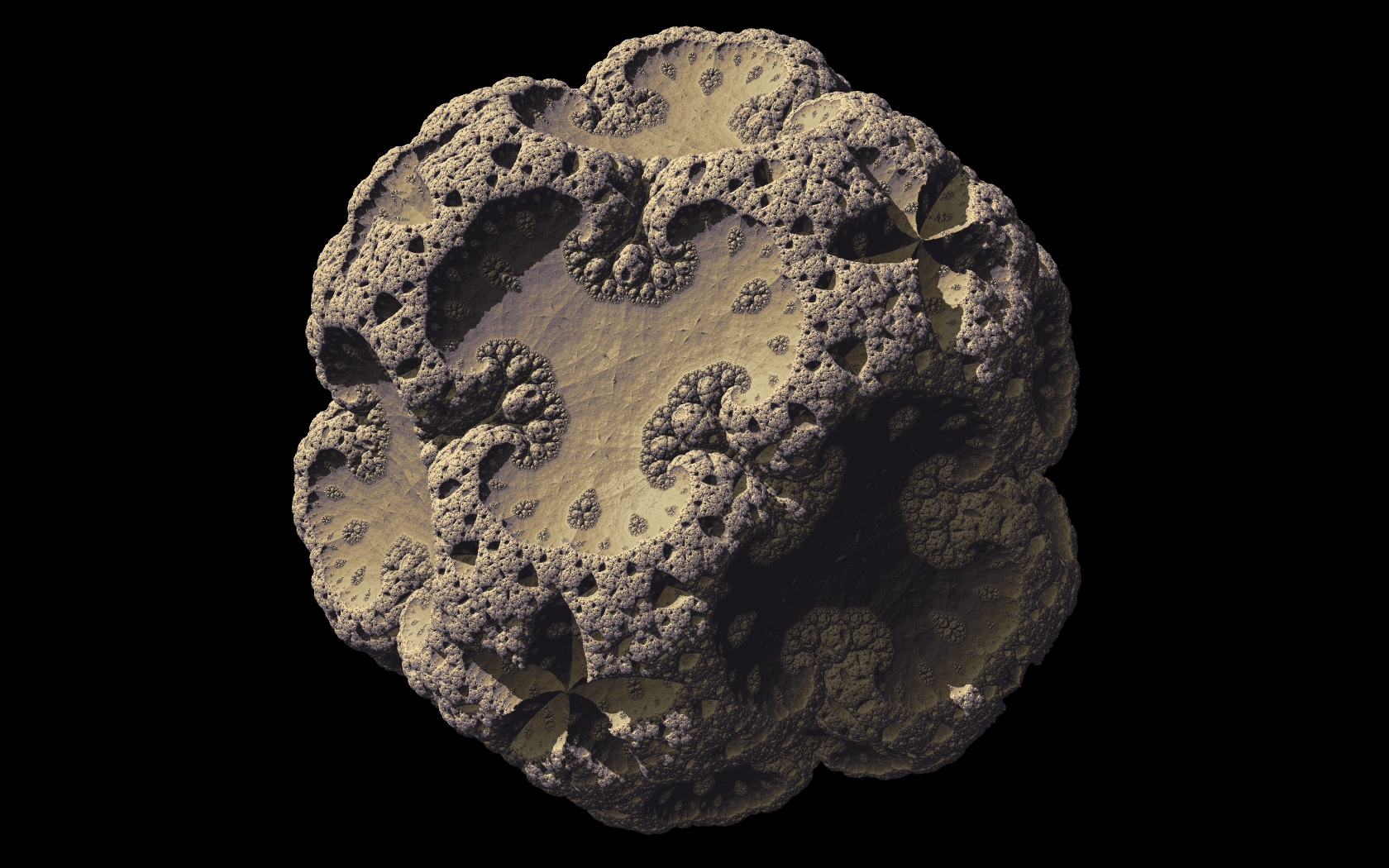 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #111 on: May 21, 2010, 11:58:24 AM » |
|
also a really nice one  I wonder what happens with aribitary symmetry planes... Maybe something along the lines of a starfish or even a more complex biological lifeform could be recreated? We already have a lot of (gorgeous) sponges.  |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #112 on: May 21, 2010, 07:37:47 PM » |
|
Yes it depends on the symmetry set choosen. If I'm not mistaken, 15 is the total number of symmetry planes of the dodeca and icosa. If you want only the icosa, 5 folds are sufficient. Same thing with the dodeca. The set that gives dodeca that way, is not the same for icosa. I've already found a "full" folding planes set for dodeca, icosa and the semi regular polyhedra that are in between. The number of folds was 9 but I think that it is possible with 8 folds.
I guess I'm a bit confused about what exactly count as a 'fold'. Do you mean you need only apply 5 conditional reflections before the scaling? Because I've only found (different) solutions with 6 conditional reflections for the icosa and dodeca. Yes, by "fold", I mean "conditional reflexion". Sorry! that was 6 for me too. According to Jos Leys 5 are sufficient if I undestood well. So far, Ive found a minimum of 5 folds for icosa and 6 folds for dodeca and 8 for full dodeca-icosa symmetry set. More infos after.  also a really nice one  I wonder what happens with aribitary symmetry planes... Maybe something along the lines of a starfish or even a more complex biological lifeform could be recreated? We already have a lot of (gorgeous) sponges.  There are already some rederings by Buddhi in this thread and this woderful gallery by Syntopia.  Thanks for the code snippets guys. That cleared everything up and I now have icosahedral and dodecahedral folding working.
Jason
<Quoted Image Removed>
You'r welcome!  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #113 on: May 22, 2010, 12:01:41 AM » |
|
Wow! Thanks for sharing  I especially like #4 and #6  #6 isn't actually that far away from a starfish, I guess  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Syntopia
|
 |
« Reply #114 on: May 22, 2010, 12:20:42 AM » |
|
Thanks, Kram and Knighty - actually I made the images after reading your suggestion to tweak the planes. And #6 was an attempt to model a starfish. Guess I did not fail completely :-) So far, Ive found a minimum of 5 folds for icosa and 6 folds for dodeca and 8 for full dodeca-icosa symmetry set. More infos after.  Oh no, that means I've been sloppy. There is really a lot of possibilities and parameters to explore here. And so many possible extensions: alternating sets of symmetries, stochastic conditionals, non-linear scaling and folds, softening the folds, ... |
|
|
|
|
 Logged
Logged
|
|
|
|
Tglad
Fractal Molossus
 
Posts: 703

|
 |
« Reply #115 on: May 22, 2010, 01:44:09 AM » |
|
#4 is almost exactly the shape of hyperbolic space.
I wonder how many of these can be made with a single fold per iteration, after-all up to 3 folds can probably be made a repeated single fold and rotation.
That would give a very simple definition for such fractals-
They are the many valued vector
v = o + q*abs(v) for some quaternion q, offset o, and where abs just operates on the real axis if we imagine the vector as (r,i,j)
|
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #116 on: May 22, 2010, 05:36:36 PM » |
|
So far, Ive found a minimum of 5 folds for icosa and 6 folds for dodeca and 8 for full dodeca-icosa symmetry set. More infos after.  Oh no, that means I've been sloppy. You weren't but I was.  Here are the 8 folding planes that fold the icosa to the fundamental triangle ( phi , 1 , 0 ) ; ( phi , 0 , 0 ) ; ( ( 2 * phi + 1 ) / 3 , 0 , phi / 3 ): ( 1 , 0 , 0 ) ( 0 , 1 , 0 ) ( 0 , 0 , 1 ) 0.5 * ( phi , 1 - phi , -1 ) ( phi , phi^2 , -( 1 + 2 * phi )) * 1 / sqrt( 14 + 6 * sqrt( 5 )) 0.5 * ( 1 , -phi , phi - 1 ) ( phi , -phi^2 , -1 ) * 1 / sqrt( 6 + 2 * sqrt(5)) ( phi , -phi^2, -( 1 + 2 * phi)) * 1 / sqrt( 14 + 6 * sqrt(5)) The five first planes give an icosahedron when the center of stretching is (phi,1,0). There is really a lot of possibilities and parameters to explore here. And so many possible extensions: alternating sets of symmetries, stochastic conditionals, non-linear scaling and folds, softening the folds, ...
May I add L-system and finite state machine... |
|
|
|
|
 Logged
Logged
|
|
|
|
knighty
Fractal Iambus
  
Posts: 819
|
 |
« Reply #117 on: May 24, 2010, 03:50:40 PM » |
|
#4 is almost exactly the shape of hyperbolic space.
I wonder how many of these can be made with a single fold per iteration, after-all up to 3 folds can probably be made a repeated single fold and rotation.
That would give a very simple definition for such fractals-
They are the many valued vector
v = o + q*abs(v) for some quaternion q, offset o, and where abs just operates on the real axis if we imagine the vector as (r,i,j)
Wow! it took me a while to understand!  I think it may be simplified further to: v:= A * abs x/y/z/xy/xz/yz/xyz(v); Where A is an affine transformation and abs() acts on x,y,z,xy,xz,yz or xyz components. 'A' may be constructed this way: A=R 1*S*T*R 2; R: rotation matrix; S: Homotety matrix; T: Translation matrix; |
|
|
|
|
 Logged
Logged
|
|
|
|
|
subblue
|
 |
« Reply #118 on: May 24, 2010, 10:23:02 PM » |
|
Wow! it took me a while to understand!  I think it may be simplified further to: v:= A * abs x/y/z/xy/xz/yz/xyz(v); Where A is an affine transformation and abs() acts on x,y,z,xy,xz,yz or xyz components. 'A' may be constructed this way: A=R 1*S*T*R 2; R: rotation matrix; S: Homotety matrix; T: Translation matrix; I can't say I understand this yet. Have you managed to code an implementation of this? |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Softology
|
 |
« Reply #119 on: May 24, 2010, 11:28:13 PM » |
|
Wow! it took me a while to understand!  I think it may be simplified further to: v:= A * abs x/y/z/xy/xz/yz/xyz(v); Where A is an affine transformation and abs() acts on x,y,z,xy,xz,yz or xyz components. 'A' may be constructed this way: A=R 1*S*T*R 2; R: rotation matrix; S: Homotety matrix; T: Translation matrix; I can't say I understand this yet. Have you managed to code an implementation of this? I would be interested in a snippet of code that covers this too if you work it out. Looks like a great way to open up even more space for finding new fractals within. Jason. |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















