|
Timeroot
|
 |
« on: March 13, 2010, 05:32:42 AM » |
|
Hi, I was just wondering what would happen if Newton's method was applied to some normal equation, like x^3+1=0, but the equation had been manipulated. That is, the roots will all stay the same, but it will be written differently. Since Newton fractals aren't about the roots, but rather just the path to them, this could lead to some interesting alterations. For example, in a simple equation with one parameter: x^3+ax+1=0 x^3=-ax-1 x^4+x^3=-ax^2-1-(a+1)x (x^4+x^3+1)/(ax^2+(a+1)x+2) + 1 = 0 This is exactly equivalent, but it's been convoluted into some other equation that will probably behave on many scales more like either a fourth or second order polynomial instead. If you applied Newton's method to this equation, you would approach the three same results, but with a completely different path. Doesn't anyone care to render this? My computer is broken, and I'm not allowed to download programs onto this one.  |
|
|
|
|
 Logged
Logged
|
Someday, man will understand primary theory; how every aspect of our universe has come about. Then we will describe all of physics, build a complete understanding of genetic engineering, catalog all planets, and find intelligent life. And then we'll just puzzle over fractals for eternity.
|
|
|
|
kram1032
|
 |
« Reply #1 on: March 13, 2010, 10:22:31 AM » |
|
the equation on this one would be  (x (a x+a+1)+2)^3}\over{a (2 (x^5-2 x^4-3 x^3+x)+1)+((x-6) x-14) x^2+1}}<br />) a would be a random constant? Hmmm... It would be interesting to see newtonians in 3D - would they stay planar and the 3D dimension would just add thickness or would the whole shape become a 3D-equivalent of the shape? Like for order 3 Newtoneans a thetraedral shape? |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Timeroot
|
 |
« Reply #2 on: March 13, 2010, 07:20:57 PM » |
|
Yes, a is just some parameter the use can select. For a regular newton, a=0, but a can be changed to get a wider range of cubics.
It depends on how you define the 3D coordinates. Derivatives aren't defined on triplex numbers, but you could still use the same formula as for complex numbers I suppose.... I think it would still preserve the x/y plane, so it would still have the three-fold symmtery, nothing tetrahedral. Maybe with a power ~2.5 you would get something like that, with three legs protruding into 3D... but I doubt it. Would be interesting to see.
|
|
|
|
|
 Logged
Logged
|
Someday, man will understand primary theory; how every aspect of our universe has come about. Then we will describe all of physics, build a complete understanding of genetic engineering, catalog all planets, and find intelligent life. And then we'll just puzzle over fractals for eternity.
|
|
|
|
kram1032
|
 |
« Reply #3 on: March 13, 2010, 08:52:41 PM » |
|
As the complex derivatives pretty much are the same as real ones, triplex ones should be the same  Well, you could easily "force" a newtonean to be interesting in all three directions by simply multiplying a polynomial up yourself. ) using triplex numbers for 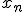  As multiplication seems to work, this should give some nice full 3D-results  However, Newtoneans admitedely aren't the most interesting fractals in the world. Except if you use a complex constant (or in this case a triplex one) which gives a LOT of interesting shapes  The pi should be a multiplication but I'm not sure how to propperly do that in LaTex^^ |
|
|
|
|
 Logged
Logged
|
|
|
|
|
reesej2
Guest
|
 |
« Reply #4 on: March 21, 2010, 01:09:49 AM » |
|
Derivatives with respect to triplex numbers ought to be more or less the same as derivatives with respect to reals. Two concerns: Do we have a rigorous definition of division for triplex numbers? And the Fundamental Theorem of Algebra guarantees that an order-N polynomial with complex coefficients has N roots in the complex plane, counting repeats. I feel like using triplex rather than complex numbers might cause something weird to happen there. Though it would certainly be interesting to try...
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Timeroot
|
 |
« Reply #5 on: March 21, 2010, 03:20:34 AM » |
|
I believe division of a/b={a.radius/b.radius,a.phi-b.phi,a.theta-b.theta}, using notation {radius,phi,theta}. I think probably many important theorems wouldn't hold true in triplex numbers, and many couldn't even be defined very well, because there are equivalent definitions of the theorem for complex numbers that are different in triplex. For example, I think (x-1)*(x+1)=/=x^2-1 in triplex numbers. I doubt you would get any triplex roots unless you had triplex coefficients, though...
|
|
|
|
|
 Logged
Logged
|
Someday, man will understand primary theory; how every aspect of our universe has come about. Then we will describe all of physics, build a complete understanding of genetic engineering, catalog all planets, and find intelligent life. And then we'll just puzzle over fractals for eternity.
|
|
|
|
reesej2
Guest
|
 |
« Reply #6 on: March 21, 2010, 05:44:59 AM » |
|
Oh yes, that definition of division works nicely.
Hm... if algebraic relations like that break down, there may be some tricky problems to deal with if we want to get much more complicated than the Mandelbulb. I actually think a triplex number could be the solution to a polynomial with complex coefficients, if of course we consider the first two coordinates of the triplex as real and imaginary components respectively--as a matter of fact, (r, theta, phi) = (cube root (2), 2pi / 3, 2pi / 3) satisfies the polynomial x^3 - 2 = 0. In fact, there are twelve strictly triplex solutions to that equation.
Back to the topic of Newton's method--with these extra solutions all over the place, does Newton's method even work at all with triplex numbers? The method's very much dependent on algebra, which is apparently kind of questionable.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #7 on: March 21, 2010, 11:13:46 AM » |
|
there's no real correctness in this case. Basically all the experiments with those numbers so far where based on the fact that complex numbers have a polar form - so triplex would have a "spherical" form, but the definitions aren't 100% consistent with x*x=x² and similar. also, (x²)³ does not necessarily equal x^6... I think, (x²)³ doesn't even equal (x³)² However, in respect to this algebra, the result counts. If you want this to be done 100% seriously, you'd need to look exactly at how the results differ from each other or what could be done to "fix" it, if that's at all possible. However, just a visual experiment of that would already be nice  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
Timeroot
|
 |
« Reply #8 on: March 21, 2010, 05:59:45 PM » |
|
Yes, I see now how there could be triplex solutions. In general, I'm guessing, if you count double roots as two separate roots, there are n2 roots to a polynomial of order n. (Remember that the latitude can't go further than +/- pi/2) With complex numbers, if we're just thinking about real coefficients, then the roots are - in some ways - just divisions of a full angle by n. In triplex numbers, the full circle is being divided in both latitude and longitude.
Hmm, due to the weird behavior of the poles, "double roots" could arrive in a totally weird fashion. Think of x^4-1=0. We have {1,0,0}, {1,pi/2,0}, {1,pi,0}, {1,3pi/4,0} - our purely complex roots - and {1,0,pi/2}, {1,0,-pi/2}, {1,pi/2,pi/2}, {1,pi/2,-pi/2}, {1,pi,pi/2}, {1,pi,-pi/2}, {1,3pi/2,pi/2}, and {1,3pi/2,-pi/2}. But of these triplex roots, there are really only two! When the latitude=+/- pi/2, the longitude is irrelevant - if you circumnavigate the globe while at Santa's house, you won't have taken a single step; just spun around on your toes. The "doubleness" is just as valid here as "regular" double roots, because they are both just as singular.
I suppose any advanced math with triplex number would be hard, because of the pole problem. I think this dissatisfies the Cauchy-Riemann equations (if they are extended), and so the derivatives wouldn't be invariant as to your "direction" in space. First think of the function x^2. It's derivative is 2x. For real numbers, this is the slope. If you want to know the slope in the complex plane in the real direction, it's still 2x. If we want to find the change in the imaginary "direction", we can just replace the x with ix and get the correct value. Now think of the function abs(x). If you wanted to specify it's derivative, for real numbers the definition {x<1, return -1;x>1, return 1} works great. In the complex plane you can't use inequalities, though, so we can define the derivative as x/abs(x). But in the complex plane this is clearly false. at x=i, the slope of |x|=0, and yet the expression suggests it would be i. Even if you do write out the full expression that "works" in the complex plane, which involves the real and imaginary parts, it's completely wrong if you try to find the slope in another "direction".
I'm worried that the same problems might occur with otherwise harmless functions such as x^3+1 when triplexes are introduced.
|
|
|
|
|
 Logged
Logged
|
Someday, man will understand primary theory; how every aspect of our universe has come about. Then we will describe all of physics, build a complete understanding of genetic engineering, catalog all planets, and find intelligent life. And then we'll just puzzle over fractals for eternity.
|
|
|
|
reesej2
Guest
|
 |
« Reply #9 on: March 21, 2010, 08:08:14 PM » |
|
I agree, any sort of rigorous mathematics with triplex numbers would be very difficult, but I think it's still possible--the fact that simple algebraic operations like that don't work is a pain, but not actually all that worrying. Quaternions have a worse problem--addition is not commutative--and there has been a great deal of rigorous mathematical study of those. Nevertheless, in order to do something as... um... fundamentally algebraic? as a Newton's Method fractal, you're going to have to either modify the numbers to fit the method or the method to fit the numbers. Shouldn't be TOO hard to manage the latter, I think...
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #10 on: March 21, 2010, 08:42:52 PM » |
|
I didn't get that last part...
|i|=0?
|i|=1, I thought...
sgn(x+y*i) = (x+y*i)/abs(x+y*i) works just fine...
the sgn function isn't really that problematic I guess. It's simply defined to be a unit-vector which points into the direction of the original vector:
sgn(x+y*i+z*j)=(x+y*i+z*j)/sqrt(x²+y²+z²)
This doesn't include any hassle and is straight forward, as 1/sqrt(x²+y²+z²) is a scalar and can be simply multiplied per element.
Maybe I got you totally wrong here, though...
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
Timeroot
|
 |
« Reply #11 on: March 21, 2010, 09:46:43 PM » |
|
I was just using abs as a badly behaved function when doing derivatives in the complex plane. For real numbers, d(|x|)/dx=x/|x| or, as you said, sgn(x). But in the complex plane this ceases to be true. At x=i, d(|x|)/dx=0. If you think of the abs function as a cone in the complex plane, x=i+Real forms a hyperbola with x=i being at its base. Thus, the d(|x|)/dx at x=i is 0, and the derivative for real values is false. In addition, if we take the derivative in the imaginary direction, that is, d(|x|)/dx where dx is purely imaginary, we get a slope of 1 again. If we take a derivative in some other direction, such as sqrt(0.5)+sqrt(0.5)i, we'll get another derivative entirely. For well behaved functions, like x^2, the slope is 2 times x for all directions. I'm afraid that, when using triplexes, even functions like x^2 will start behaving badly too.
Reesej2, I believe you meant quaternions aren't commutative with regards to multiplication. That's a good point, maybe hints to triplexes lie in quaternions... *looks wistfully up at the sky*
|
|
|
|
|
 Logged
Logged
|
Someday, man will understand primary theory; how every aspect of our universe has come about. Then we will describe all of physics, build a complete understanding of genetic engineering, catalog all planets, and find intelligent life. And then we'll just puzzle over fractals for eternity.
|
|
|
|
kram1032
|
 |
« Reply #12 on: March 21, 2010, 10:55:14 PM » |
|
I still don't see the problem:
the first derivative is meant to be the slope of the function. (I hope, I'm using the correct term here^^)
at x<0, the function constantly falls with k=-1
at x>0, the function constantly increases with k=1
at (x+y*i) with x=0 and y>0, at first glance, the result would be undefined. On the second glance, it rises with i and rises with -i at y<0 respectively.
So, as I see it, the slope of abs(z) always is sgn(z), no matter which circumstances...
At least for complex numbers^^
Maybe I don't get an important part...
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
reesej2
Guest
|
 |
« Reply #13 on: March 21, 2010, 11:15:17 PM » |
|
Whoops, my mistake, it is indeed multiplication. Which is actually pretty similar to the problems we're encountering here.
Kram1032: What Timeroot is pointing out is that the _direction_ in which you consider a derivative matters. The derivative at i is 0 if you try to head in the direction of the reals (so, at an angle of zero) but 1 if you go "north" or "south" (angle of pi/2).
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
kram1032
|
 |
« Reply #14 on: March 21, 2010, 11:41:42 PM » |
|
Oh, I see! A directional derivative  Ok, point taken  |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















