|
Aexion
|
 |
« on: July 20, 2011, 03:00:07 AM » |
|
Hello, I have been experimenting lately with some higher dimensional systems based on the platonic solids and here are some of my results. I have used the mandelbox equation for all of them, since its very simple to use. But you can also use others..  The formulas are in simple C format and in most cases, I didn't have optimized them in order to maintain clarity. Tetrahedron/OctahedronI have posted this formula before, its on the Quadray post. The main difference between the old formula and the presented one is the fact that setting the delta value to 3, generates the tetrahedron, while a value of 0 generates the octahedron (also, this is array based, the old one used variables). Here is the formula: bool TetraOcta(float x, float y, float z,int Iter){
bool escape=false;
float V[4];//variables
float CT[4];//C Value
float radius=0;
int ic;
const float delta=3;//make it 0 for the octahedron
//four dimensions
CT[0]=fabs((x+y+z)-delta);
CT[1]=fabs((-x-y+z)-delta);
CT[2]=fabs((-x+y-z)-delta);
CT[3]=fabs((x-y-z)-delta);
for(int it=0;it<4;it++)V[it]=0;
for (ic=0;ic<Iter;ic++){
radius=0;
for(int it=0;it<4;it++){
if(V[it]>1)V[it]=2-V[it];
else
if(V[it]<-1)V[it]=-2-V[it];
radius+=(V[it]*V[it]);
}
const float vm=sqrt(radius);
if(vm<0.5){
for(int it=0;it<4;it++)V[it]*=4;
} else
if(vm<1){
const float vsq=vm*vm;//-vm*vm for fun!!
for(int it=0;it<4;it++)V[it]/=vsq;
}
radius=0;
for(int it=0;it<4;it++){
V[it]=V[it]*2+CT[it];
radius+=(V[it]*V[it]);
}
if (radius>3600) break;
}
if(ic<Iter)escape=false;else escape=true;
return escape;
}
 I have another Octahedron formula (6D) but its slower than this one.. For the Cube, well, everyone knows the Mandelbox, so I will skip it.. Now here comes the more complicated ones..I warn you..those formulas are not for the faint of heart, since they have more than the classic 3D  Dodecahedron DodecahedronThis is a large formula, it has 12 Dimensions and if you plan to render it, I recommend you to use GPU.. bool Dodecahedron(float x, float y, float z,int Iter){
bool escape=false;
float V[12];//variables
float CT[12];//C Value
float radius=0;
int ic;
const float delta=7;
//12 Dimensions
CT[0]=fabs(y+z*1.6180339887498948482045868343656)-delta;
CT[1]=fabs(-y+z*1.6180339887498948482045868343656)-delta;
CT[2]=fabs(y-z*1.6180339887498948482045868343656)-delta;
CT[3]=fabs(-y-z*1.6180339887498948482045868343656)-delta;
CT[4]=fabs(x+y*1.6180339887498948482045868343656)-delta;
CT[5]=fabs(-x+y*1.6180339887498948482045868343656)-delta;
CT[6]=fabs(x-y*1.6180339887498948482045868343656)-delta;
CT[7]=fabs(-x-y*1.6180339887498948482045868343656)-delta;
CT[8]=fabs(x*1.6180339887498948482045868343656+z)-delta;
CT[9]=fabs(-x*1.6180339887498948482045868343656+z)-delta;
CT[10]=fabs(x*1.6180339887498948482045868343656-z)-delta;
CT[11]=fabs(-x*1.6180339887498948482045868343656-z)-delta;
for(int it=0;it<12;it++)V[it]=0;
for (ic=0;ic<Iter;ic++){
radius=0;
for(int it=0;it<12;it++){
if(V[it]>1)V[it]=2-V[it];
else
if(V[it]<-1)V[it]=-2-V[it];
radius+=(V[it]*V[it]);
}
const float vm=sqrt(radius);
if(vm<0.5){
for(int it=0;it<12;it++)V[it]*=4;
} else
if(vm<1.5){
const float vsq=vm*vm;//-vm*vm for fun!!
for(int it=0;it<12;it++)V[it]/=vsq;
}
radius=0;
for(int it=0;it<12;it++){
V[it]=V[it]*2+CT[it];
radius+=(V[it]*V[it]);
}
if (radius>3600) break;
}
if(ic<Iter)escape=false;else escape=true;
return escape;
}
Here is an example render of this formula (its the same that I have posted on the Quadray post)  You can also see it near the center (I have post a render on DA): http://aexion.deviantart.com/art/Near-the-Core-207032701IcosahedronThis formula is..well.. it's complicated.. mostly because it has 20 dimensions.. bool Icosahedron(float x, float y, float z,int Iter){
bool escape=false;
float V[20];//variables
float CT[20];//C Value
float radius=0;
int ic;
const float delta=0;
//20 dimensions
CT[0]=fabs(x+y+z)-delta;
CT[1]=fabs(x+y -z)-delta;
CT[2]=fabs(x -y +z)-delta;
CT[3]=fabs(x -y -z)-delta;
CT[4]=fabs(-x+ y +z)-delta;
CT[5]=fabs(-x +y -z)-delta;
CT[6]=fabs(-x -y +z)-delta;
CT[7]=fabs(-x -y -z)-delta;
CT[8]=fabs(y*0.61803398874989484820458683436564+ z*1.6180339887498948482045868343656)-delta;
CT[9]=fabs(y*0.61803398874989484820458683436564 -z*1.6180339887498948482045868343656)-delta;
CT[10]=fabs(-y*0.61803398874989484820458683436564 +z*1.6180339887498948482045868343656)-delta;
CT[11]=fabs(-y*0.61803398874989484820458683436564 -z*1.6180339887498948482045868343656)-delta;
CT[12]=fabs(x*0.61803398874989484820458683436564+ y*1.6180339887498948482045868343656)-delta;
CT[13]=fabs(x*0.61803398874989484820458683436564 -y*1.6180339887498948482045868343656)-delta;
CT[14]=fabs(-x*0.61803398874989484820458683436564 +y*1.6180339887498948482045868343656)-delta;
CT[15]=fabs(-x*0.61803398874989484820458683436564 -y*1.6180339887498948482045868343656)-delta;
CT[16]=fabs(x*1.6180339887498948482045868343656 + z*0.61803398874989484820458683436564)-delta;
CT[17]=fabs(x*1.6180339887498948482045868343656 -z*0.61803398874989484820458683436564)-delta;
CT[18]=fabs(-x*1.6180339887498948482045868343656 +z*0.61803398874989484820458683436564)-delta;
CT[19]=fabs(-x*1.6180339887498948482045868343656 -z*0.61803398874989484820458683436564)-delta;
for(int it=0;it<20;it++)V[it]=0;
for (ic=0;ic<Iter;ic++){
radius=0;
for(int it=0;it<20;it++){
if(V[it]>1)V[it]=2-V[it];
else
if(V[it]<-1)V[it]=-2-V[it];
radius+=(V[it]*V[it]);
}
const float vm=sqrt(radius);
if(vm<0.5){
for(int it=0;it<20;it++)V[it]*=4;
} else
if(vm<1.75){
const float vsq=vm*vm;
for(int it=0;it<20;it++)V[it]/=vsq;
}
radius=0;
for(int it=0;it<20;it++){
V[it]=V[it]*2+CT[it];
radius+=(V[it]*V[it]);
}
if (radius>3600) break;
}
if(ic<Iter)escape=false;else escape=true;
return escape;
}
And here is how it looks  I'm working with those formulas because there are some very interesting surprises on the higher dimensional spaces (did you remember the quadray mandelbrots?..  ) I also have the Sphere and a Donnut, if anyone is interested, please let me know and I will post them |
|
|
|
« Last Edit: July 20, 2011, 09:38:31 AM by Aexion »
|
 Logged
Logged
|
 | Fractals all the way..
Incendia for 3D Fractals
Aural for Musical Fractals |
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #1 on: July 20, 2011, 10:49:49 AM » |
|
The "problem" with those formulas is mainly that they don't mix well with the older ones so I tried to modify them with more "standard" transform types  But what about those variants? I was wondering about ... . n sided pyramid . n sided extruded polyhedron . cone . cylinder  I was thinkin about using my PolyfFolding for it but it uses a kind of abs thing... So it's better to do many consecutive rotations  |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
|
Aexion
|
 |
« Reply #2 on: July 20, 2011, 11:26:07 AM » |
|
The "problem" with those formulas is mainly that they don't mix well with the older ones so I tried to modify them with more "standard" transform types  But what about those variants? I was wondering about ... . n sided pyramid . n sided extruded polyhedron . cone . cylinder  I was thinkin about using my PolyfFolding for it but it uses a kind of abs thing... So it's better to do many consecutive rotations  Oh, they will really not mix with their lower dimensional counterparts..the reason..well..its just like the old joke of the ant and the elephant.. I mean, the Icosahedral formula is 20D, while the original box is 3D.. Size matters..  As for the others, well, you already implemented the extruded hexagon: http://www.fractalforums.com/3d-fractal-generation/quadray-sets/msg32005/#msg32005Pyramids can be a variant of the hexagon and cylinders can be easy devised from the Golden Donnut: http://aexion.deviantart.com/art/The-Golden-Donnut-210148578As for the folding, I have a quadray fold, that turns the 3d point into a quadray, calculates the folding and then applies the inverse quadray transform, in order to return to 3D.. there are variants for the higher dimensional, but I'm still creating their inverse forms.. |
|
|
|
|
 Logged
Logged
|
 | Fractals all the way..
Incendia for 3D Fractals
Aural for Musical Fractals |
|
|
|
|
KRAFTWERK
|
 |
« Reply #3 on: July 20, 2011, 02:14:50 PM » |
|
Interesting stuff, and beautiful images Aexion! 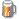 |
|
|
|
|
 Logged
Logged
|
|
|
|
|
ant123
Guest
|
 |
« Reply #4 on: September 04, 2011, 12:03:14 AM » |
|
DODECAHEDRONS LOOK REALLY AMAZING!!! I was just thinking the same thing. Does the mandelbox actually use euclidian spacial geometry? so you are saying, fold planes YZ this way and fold planes XZ that way? in that case could you also fold the mandelbox according to different planes like those in dodecahedrons and tetrahedrons? that would look pretty amazing! 5 sided 3d geometries are fantastically pleasing to look at. can you make a trapezoid mandelbox? And what about dodecahedral and octahedral menger sponges? someone feel free to make some recursive functions of these guys: https://picasaweb.google.com/114142284069986068206/September32011#5648173911170210850      <<<<<<<<<<<<<< |
|
|
« Last Edit: September 04, 2011, 12:14:21 AM by ant123 »
|
 Logged
Logged
|
|
|
|
|
|
|
ant123
Guest
|
 |
« Reply #6 on: September 06, 2011, 12:55:04 AM » |
|
Very nice pics!!!!!
What about folding with mixed polyhedron shapes, cube, tetrahedron and octrahedron in the same folding algorythm? and introducing a spiral element into the folding, i.e. every time rotate the folding angles by 1 degrees relative to a central point, axis, etc, and transforming the folding planes outwards, right, up, etc. ?
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
jehovajah
|
 |
« Reply #7 on: September 06, 2011, 01:46:50 AM » |
|
These images illustrate the notion of dimensionality is not that of perpendicular directions, but rather that of orthogonal directions. The difference is the difference between generalised coordinates and 3d rectilinear coordinates.
The significance of this is that Euclidean geometry has come of age, and its fundamental, fractal basis has been revealed in glorious, gorgeous colour,
There is a second no less significant evolution: the ability to apprehend the subjective viewpoint, and the subjective processing that takes place in computing the output surfaces, colours and intensities.
You do not need to stop there, as haptic programme codes will give you the force models to feel these fractal forms, stereoscopic and stereo audition codes the ability to see and hear these foms in space,
This is how far we have come, and you gentlemen are at the bleeding edge of a brave new fractal worldview.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
Syntopia
|
 |
« Reply #8 on: September 22, 2011, 11:38:22 PM » |
|
None was interested (on implementing it)
Hi, Aexion, your systems are very interesting! We just haven't had the time :-) I tried it today and arrived at this compact scalar DE implementation for the tetra/octa thing: float DE(vec3 p) {
vec4 CT = abs(vec4(p.x+p.y+p.z-delta,-p.x-p.y+p.z-delta,-p.x+p.y-p.z-delta,p.x-p.y-p.z-delta));
vec4 V = vec4(0.0);
float V2 = 0.0, dr = 2.0;
for (int i=0;i<Iterations;i++){
V = clamp(V, -1.0, 1.0) * 2.0 - V;
V2 = dot(V,V);
float c = clamp(max(0.25/V2, 0.25), 0.0, 1.0)/0.25;
V*=c; dr/=c;
V=V*2.0+CT; dr/=2.0;
if (V2>3600.0) break;
}
return dr*sqrt(V2);
}
It was very surprising to me that the ordinary Mandelbox DE worked - since we return the length (and running derivative) of tetrahedron coordinates, and use these as a distance estimate in our normal 3D coordinates. |
|
|
|
|
|
Aexion
|
 |
« Reply #9 on: September 23, 2011, 12:48:56 AM » |
|
None was interested (on implementing it)
Hi, Aexion, your systems are very interesting! We just haven't had the time :-) I tried it today and arrived at this compact scalar DE implementation for the tetra/octa thing: It was very surprising to me that the ordinary Mandelbox DE worked - since we return the length (and running derivative) of tetrahedron coordinates, and use these as a distance estimate in our normal 3D coordinates. Many Thanks!!  I didn't have explored much these sets (no time too!.), but I suspect that they have many interesting possibilities, but lately I have found that if you change the spherefold by another 3d surface, the result is.. well see for yourself: bool Surfacefold(double x, double y, double z,int miter){
const double ctx =x;
const double cty =y;
const double ctz =z;
x=0;
y=0;
z=0;
for(unsigned char Counter=0;Counter<miter;Counter++){
if(x>1)x=2-x;
else
if(x<-1)x=-2-x;
if(y>1)y=2-y;
else
if(y<-1)y=-2-y;
if(z>1)z=2-z;
else
if(z<-1)z=-2-z;
/*
const float rw=(cos(x) * sin(y) + cos(y) * sin(z) + cos(z) * sin(x))*3.141592653;//Gyroid
const float vm=rw;// vm=-rw; vm=fabs(rw);
*/
const float rw=-(x*x + y*y + z*z) +cos(5*x)+cos(5*y)+cos(5*z) -.1; //Bloby Schwartz surface from K3DSurf
const float vm=-rw; // vm=fabs(rw);
if(vm<0.5){
x=x*4;
y=y*4;
z=z*4;
} else
if(vm<1){
const float vsq=vm*vm;
x/=vsq;
y/=vsq;
z/=vsq;
}
x=x*2+ctx;
y=y*2+cty;
z=z*2+ctz;
if ((x*x+y*y+z*z)>3600) break;
}
if((x*x+y*y+z*z)<3600)
return true;
else
return false;
}
Try the Gyroid version..  There are many 3d surfaces to explore.. |
|
|
|
|
 Logged
Logged
|
 | Fractals all the way..
Incendia for 3D Fractals
Aural for Musical Fractals |
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #10 on: September 23, 2011, 12:40:03 PM » |
|
 Well I tried to put it in MB it looks interesting... But only at neg scale and with minr>0.5 afaik. the render is a bit slow (not too much)
|
No sweat, guardian of wisdom!
|
|
|
|
Aexion
|
 |
« Reply #11 on: September 23, 2011, 02:43:48 PM » |
|
 Well I tried to put it in MB it looks interesting... But only at neg scale and with minr>0.5 afaik. the render is a bit slow (not too much) Oh, try the other functions.. Meanwhile, here is a Mandelbox made of.. Hearts!!!, if you want to spread love trough the fractal universe  (actually, gravity does a better job, because while love attracts, it often breaks, while gravity never fails) Works very well with low iterations.. double Heart( double x,double y,double z )
{
double xx = x*x;
double yy = y*y;
double zz = z*z;
double a = 2*xx + yy +zz - 1;
a = a*a*a;
zz *= z;
return a - 0.1*xx*zz - yy*zz;
};
bool HeartBox(double x, double y, double z,int miter){
const double ctx =x;
const double cty =y;
const double ctz =z;
x=0;
y=0;
z=0;
for(unsigned char Counter=0;Counter<miter;Counter++){
if(x>1)x=2-x;
else
if(x<-1)x=-2-x;
if(y>1)y=2-y;
else
if(y<-1)y=-2-y;
if(z>1)z=2-z;
else
if(z<-1)z=-2-z;
const float h=Heart(z,x,y)*0.0005;//size of love
const float rw=x*x+y*y+z*z;
const float vm=sqrt(rw*h);//-sqrt(rw*h);//reverse it
if(vm<0.5){
x=x*4;
y=y*4;
z=z*4;
} else
if(vm<1){
const float vsq=vm*vm;
x/=vsq;
y/=vsq;
z/=vsq;
}
x=x*2+ctx;
y=y*2+cty;
z=z*2+ctz;
if ((x*x+y*y+z*z)>3600) break;
}
if((x*x+y*y+z*z)<3600)
return true;
else
return false;
}
I got the Heart function from Paul Bourke Website: http://paulbourke.net/geometry/heart2/ |
|
|
|
« Last Edit: September 23, 2011, 03:29:45 PM by Aexion »
|
 Logged
Logged
|
 | Fractals all the way..
Incendia for 3D Fractals
Aural for Musical Fractals |
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #12 on: September 23, 2011, 04:01:02 PM » |
|
|
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
DarkBeam
Global Moderator
Fractal Senior
     
Posts: 2512
Fragments of the fractal -like the tip of it
|
 |
« Reply #13 on: September 23, 2011, 04:50:07 PM » |
|
Anyway, I optimized the formula (calculating sin&cos in one shot to gain speed), and found a way to reduce the busy and discontinue aspect of the fractal in a simple way. rho = sqrt(x*x+y*y+z*z); // the radius theta = cos(f*x) * sin(f*y) + cos(f*y) * sin(f*z) + cos(f*z) * sin(f*x); r = theta * Amp + rho * Rmul; When adopting this expression I noted that for a lower frequency (0.3 seems to be a good value) the fractal begins to look more harmonious.  I only need to implement the "cos(f*x)+cos(f*y)+cos(f*z)" terms, adding another Amplitude value.  Test renders soon! |
|
|
|
|
 Logged
Logged
|
No sweat, guardian of wisdom!
|
|
|
Mrz00m
Fractal Lover
 
Posts: 204
|
 |
« Reply #14 on: September 20, 2015, 10:02:05 PM » |
|
|
|
|
|
|
 Logged
Logged
|
|
|
|
|


















