|
jehovajah
|
 |
« Reply #375 on: November 08, 2009, 09:05:07 AM » |
|
 Thanks Twinbee. Found some of your motivation here just before you posted http://www.fractalforums.com/mandelbrot-and-julia-set/variety-of-the-mandelbrot-set/. Great stuff you are rendering.so i am definitely hooked. Catch up with you later.
|
|
|
|
|
 Logged
Logged
|
May a trochoid of ¥h¶h iteratively entrain your Logos Response transforming into iridescent fractals of orgasmic delight and joy, with kindness, peace and gratitude at all scales within your experience. I beg of you to enrich others as you have been enriched, in vorticose pulsations of extravagance!
|
|
|
|
twinbee
|
 |
« Reply #376 on: November 08, 2009, 03:24:49 PM » |
|
Article finished <wipes brow>: Linky: The Unravelling of the Real 3D MandelbulbA deep zoom rendering of a certain spiral has been rendered too (featured on the 2nd page). If anyone here would like to change a featured pic of theirs, let me know. Equally, any comments, suggestions, or even criticism is welcome! |
|
|
|
« Last Edit: November 08, 2009, 03:35:56 PM by twinbee »
|
 Logged
Logged
|
|
|
|
|
Buddhi
|
 |
« Reply #377 on: November 08, 2009, 04:40:08 PM » |
|
Article finished <wipes brow>: Linky: The Unravelling of the Real 3D MandelbulbA deep zoom rendering of a certain spiral has been rendered too (featured on the 2nd page). If anyone here would like to change a featured pic of theirs, let me know. Equally, any comments, suggestions, or even criticism is welcome! I have seen your website with article about 3D Mandelbrots. It is wonderful! You are the Master! |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #378 on: November 08, 2009, 05:03:11 PM » |
|
Article finished <wipes brow>: Linky: The Unravelling of the Real 3D MandelbulbA deep zoom rendering of a certain spiral has been rendered too (featured on the 2nd page). If anyone here would like to change a featured pic of theirs, let me know. Equally, any comments, suggestions, or even criticism is welcome! Hi Daniel, very nice article. You may wish to add a link to this large degree 4 render: http://makinmagic.deviantart.com/art/Asteroid-National-Park-139905412Apologies if it's already there, if it is I missed it. Also a render I did of the degree 7 entitled "7th level Mandelbrot Temple" was chosen as one of the winners in the 2009 Benoit Mandelbrot Fractal Art Contest and will be exhibited with the other winners at ICM2010: http://www.fractalartcontests.com/2009/winners.phphttp://www.icm2010.org.in/Note that in the text to go with the contest image I invited viewers to attempt to prove whether or not the White/Nylander integer degree Mandelbrots are connected, and if connected are they toplogically spheres  |
|
|
|
« Last Edit: November 08, 2009, 05:05:36 PM by David Makin »
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #379 on: November 08, 2009, 09:12:22 PM » |
|
Thanks guys!  David, congrats about the contest! Link's down at the mo - I'll try again later. Although I might prefer the coloring of the Alien Coral - you're right - the Asteroid is more advanced overall. I've added it  Garth, I've also added your latest. Note that in the text to go with the contest image I invited viewers to attempt to prove whether or not the White/Nylander integer degree Mandelbrots are connected, and if connected are they toplogically spheres That old chestnut eh? Hehe, they'll have a job  |
|
|
|
« Last Edit: November 08, 2009, 09:16:37 PM by twinbee »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #380 on: November 08, 2009, 09:23:22 PM » |
|
Note that in the text to go with the contest image I invited viewers to attempt to prove whether or not the White/Nylander integer degree Mandelbrots are connected, and if connected are they toplogically spheres That old chestnut eh? Hehe, they'll have a job  Well if no-one attending the ICM can solve it..... |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #381 on: November 08, 2009, 09:39:12 PM » |
|
David, congrats about the contest! Link's down at the mo - I'll try again later.
Thanks, and it's working again now (at least it is here). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #382 on: November 09, 2009, 02:19:45 AM » |
|
If anyone here would like to change a featured pic of theirs, let me know. Equally, any comments, suggestions, or even criticism is welcome!
Just a suggestion - where you discuss the formula you could also mention Jos Leys' algorithm for accurate analytical DE for the formula (and related formulas such as Garth Thornton's variations and Rudy Rucker's formula). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
JosLeys
|
 |
« Reply #383 on: November 09, 2009, 10:45:52 AM » |
|
I've read the article. Great overview! As to the distance estimation formula that I'm using, it may still be buggy. I was looking at the large size pictures of the degree 8 and comparing to what I'm getting in my Ultrafractal routine. It seems that with my algorithm, the buds are on 'stalks', and I can see through them (see the images below). I think this might be a rendering error, but I have not figured it out yet.. Any comments from the rendering experts?     |
|
|
|
|
 Logged
Logged
|
|
|
|
|
bib
|
 |
« Reply #384 on: November 09, 2009, 10:54:28 AM » |
|
Article finished <wipes brow>: Linky: The Unravelling of the Real 3D MandelbulbA deep zoom rendering of a certain spiral has been rendered too (featured on the 2nd page). If anyone here would like to change a featured pic of theirs, let me know. Equally, any comments, suggestions, or even criticism is welcome! Congratulations for this superb summary of the state-of-the-art. I have 2 questions : - In the 8-power monster, although the level of detail is infinite, I have the feeling that shapes do not vary as much as in the 2D M-set (2 or 8 power, it does not matter) when you zoom in. All is very self similar, and there is not such variery as you can find for example when you zoom near a minibrot in 2D. What do you think about that? - Although I have not much time to play with the maths (I could, because I did a lot of maths when I was younger, but I prefer the beauty of images rather than the beauty of equations) I would love to explore this fractal. I understand you developped your own program. @David Makin (or anybody else) : do you use Ultrafractal for your beautiful images in this thread? If so, would you mind sharing the formula ? Thanks! |
|
|
|
|
 Logged
Logged
|
Between order and disorder reigns a delicious moment. (Paul Valéry)
|
|
|
|
David Makin
|
 |
« Reply #385 on: November 09, 2009, 11:09:46 AM » |
|
@David Makin (or anybody else) : do you use Ultrafractal for your beautiful images in this thread? If so, would you mind sharing the formula ?
Thanks!
Am still working on the formula, so far I've only given Trifox a copy and he'll probably attest to the fact that it's not really ready for public release yet - I've still to sort out the parameters correctly, add more options and get all the options I've added so far as parameters working properly - I'm hoping to have a "release version" by the end of this week. Note that I didn't originally intend this formula for public release since I was just using it to fine-tune ideas for when I do a suite of class-based general ray-tracing formulas. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #386 on: November 09, 2009, 11:11:53 AM » |
|
I've read the article. Great overview!
As to the distance estimation formula that I'm using, it may still be buggy.
I was looking at the large size pictures of the degree 8 and comparing to what I'm getting in my Ultrafractal routine.
It seems that with my algorithm, the buds are on 'stalks', and I can see through them (see the images below).
I think this might be a rendering error, but I have not figured it out yet..
Any comments from the rendering experts?
Hi Jos, I'm confused by your renders, I seem to get the same results using your analytical method as I do with my delta method. Are those renders of the degree 8 ? |
|
|
|
|
 Logged
Logged
|
|
|
|
|
JosLeys
|
 |
« Reply #387 on: November 09, 2009, 11:23:26 AM » |
|
Yes Dave, it is the degree 8.
So you do not see the 'holes' with both methods, is that what you are saying?
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #388 on: November 09, 2009, 11:37:22 AM » |
|
Yes Dave, it is the degree 8.
So you do not see the 'holes' with both methods, is that what you are saying?
Am just checking what happens when I go closer to "inside" on the degree 8 than I've done previously..... |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #389 on: November 09, 2009, 11:51:37 AM » |
|
Yes Dave, it is the degree 8.
So you do not see the 'holes' with both methods, is that what you are saying?
Am just checking what happens when I go closer to "inside" on the degree 8 than I've done previously..... Hi Jos, no I definitely do not get the "holes" that you are getting, I suspect the problem is the one you mentioned to me previously where there are locations at which the analytical DE gets very large due to singularities in the derivative. Here's a quick render of the degree 8, "straight on" view but zoomed to a bud on the edge - I get no holes using your analytical method even with the threshold set very small at 1e-6. 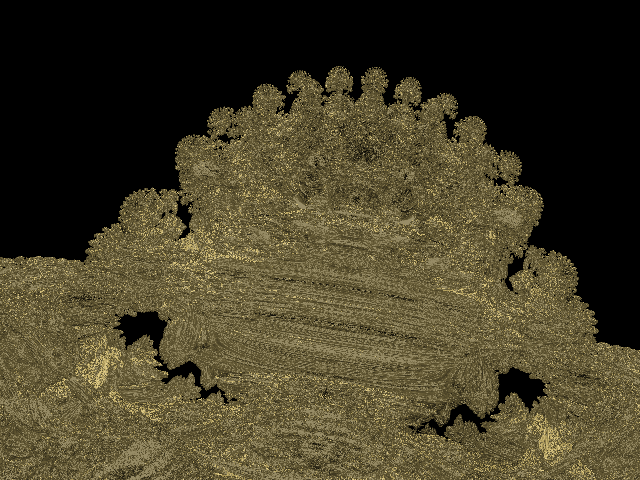 Note however that I am using the method of not stepping further at a given iteration depth on a given ray than was stepped previously at that depth on that ray *and using the array code that I sent you earlier* - I suspect your holes are due to more limited storage/checking of the step distances at iteration depth - see the code I sent you in the E-mail and see if that removes the holes. |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















