|
twinbee
|
 |
« on: September 22, 2007, 11:05:02 AM » |
|
Hi all!
I'm relatively new to fractals, but I have searched for hours to find a true 3D mandlebrot type fractal, all in vain. I don't want the raised mountain type of mandlebrot, and I don't want any true (but trivially simple) ones such as the Menger sponge. I instead want a true 3D equivalent of the mandlebrot (or near enough).
The closest I got was the Quasi-fuchsian sphere fractal:
<a href="http://www.youtube.com/v/3lcO9zRCv-4&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/3lcO9zRCv-4&rel=1&fs=1&hd=1</a>
However, that is still mostly self-similar. I want the amazing variety that can be found in the mandlebrot. Anything out there?
|
|
|
|
« Last Edit: October 19, 2009, 10:26:23 AM by Trifox »
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #1 on: September 22, 2007, 11:11:31 AM » |
|
heya, welcome to the forums. curiously i was just watching arthur clarke describing the mandelbrot set in "fractals - the colors of infinity"  there doesn't seem to be a direct 3d analogue of the mandelbrot set. you can spin it about the x axis, you can use the same kind of iteration using quaternions, and a whole bunch of other "nartural" extensions ... but in the end the character of the original mandelbrot set is lost. i've found this is true of 3d fractals in general: it's a bit of a double-edged sword, you gain some things (potentially in realism, structure) but you often lose others (simplicity, especially of exploration). to me the solution is simple: accept the mandelbrot set for what it is, be satisfied and don't try to boost it to 3 dimensions artificially. there are plenty of exciting fractals that exist natively in 3-space, and we shouldn't try to create new fractals with the expectation of looking like old ones  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #2 on: September 25, 2007, 08:16:44 AM » |
|
Thanks so much for your reply!
Even if it wasn't like a 3D rendition of the Mandelbrot, I would love to know of a 3D fractal that has mandelbrot-type beauty and complexity along with the amazing variety. As far as I know, no such fractal exists, but perhaps I haven't looked hard enough?
|
|
|
|
« Last Edit: September 25, 2007, 09:14:05 AM by twinbee »
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #3 on: September 30, 2007, 10:08:52 PM » |
|
I've just spent an exhausting week trying to create a TRUE 3D rendition of the Mandelbrot (or whatever the equivalent would turn out to be). It's been a really cumbersome, if somewhat exciting journey. Although you say we should be happy with the 2D version (which I am), I believe that maths can do anything, and that it's just a matter of finding the right equations to find the jackpot. To aid me in my quest for 3D perfection, I have tried to use 3 dimensional numbers, and have even creating my own arithmetic around it. At first I was meddling with the basic 2D formula, but trying to mould it into 3D dimensions using simple algebra (expand the equation and simplify). This leads on to questions such as what you would do if faced with i multiplied by j (j being the 3 dimensional imaginary number). Using solutions based around this approach I got some interesting extruded/distorted 3D Mandelbrot objects, but nothing like what I was hoping for (where the Mandel-type detail is surfacing throughout all 3 dimensions). Failing that, I also tried to visualize what happens in standard complex multiplications, and used rotation techniques, but in all 3 dimenions, instead of the 2D rotation for complex numbers. In the end, I got another "extruded Mandelbrot" which had a sort of bird shape at one cross section of the 3D object. It was quite interesting, but nothing sensational. Well that's it. Having done all that, I feel fairly gutted, having failed  Still it was quite fun too. If anyone has any inkling whether 3D mandelbrots could even theoretically be possible, I would love to hear. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #4 on: October 01, 2007, 12:57:36 AM » |
|
You could probably get what you're aiming for by performing fancy transforms on 3D/4D space prior to plugging coords into quaternionic iteration, though you might consider that as "cheating"  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #5 on: October 01, 2007, 01:09:31 AM » |
|
I've had a good look over the net and couldn't see anything coming even close. Even quaternionic fractals (as cool as they are), have mandelbrot-depth fractal complexity in only 1 dimension (they look very 'smooth' on the other two axes - which resemble the extruded 3D fractals I was able to create with 'triplex' numbers as I explained in my post above). In fact, they look like whipped cream  No, sorry, I'm after mandelbrot style complexity in all 3 dimensions. Something similar to the Quasi-fuchsian sphere fractal here:
<a href="http://www.youtube.com/v/3lcO9zRCv-4&rel=1&fs=1&hd=1" target="_blank">http://www.youtube.com/v/3lcO9zRCv-4&rel=1&fs=1&hd=1</a>(except that's mostly self-similar, so it's good but no cigar). |
|
|
|
« Last Edit: October 01, 2007, 01:18:14 AM by twinbee »
|
 Logged
Logged
|
|
|
|
|
David Makin
|
 |
« Reply #6 on: October 01, 2007, 01:44:32 AM » |
|
I know standard quaternionics is no use, but to go back to 2D, you could apply a 2D manipulation of the complex plane (i.e. x and y coords) prior to plugging them into the standard z^2+c iteration to (for example) give the Mandelbrot an extra lobe - or remove a lobe. In the same way you could manipulate 3D/4D space prior to plugging the coords into a quaternionic iteration (for "roundy" results) or a hypercomplex iteration (for "squarey" results) to produce 3D lobes. As you say though I've seen no-one try this yet  In fact I've never seen any 3D/4D fractal software that allows 3D/4D transformations to be applied in that way (i.e. like UXFs are used for 2D in Ultrafractal). |
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #7 on: October 01, 2007, 01:49:36 AM » |
|
Wow, sounds good. Seriously, if you see any picture on the net, then please let us know ASAP!
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #8 on: November 15, 2007, 05:22:26 AM » |
|
So far, this is the closest I've come to creating a 3D-style mandelbrot with bulbs on all axis. It uses techniques described in my "Meet & greet" forum thread, and orthographic projection with lighter areas at the front. 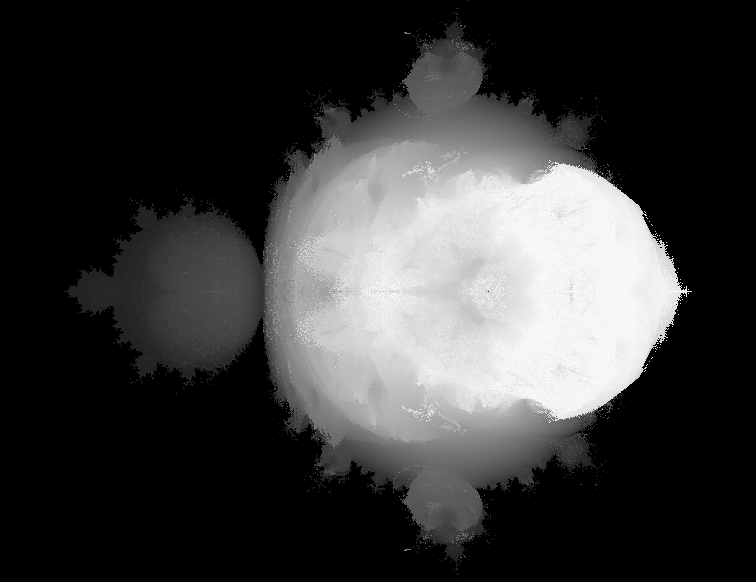 Sigh, so close, yet so far! |
|
|
|
« Last Edit: November 15, 2007, 05:41:12 AM by twinbee »
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #9 on: November 15, 2007, 08:02:02 AM » |
|
hey that's looking promising, email me the cayley table you used and i'll ray trace it - busy working on the program now after my horrible exam earlier today.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
twinbee
|
 |
« Reply #10 on: November 17, 2007, 02:52:35 PM » |
|
Hope the exam went okay. Here's the way to create the object. I'm not sure how Cayley tables would fit in this context, but here's the multiplication function:
double pi=3.14159265;
double r = sqrt(x*x + y*y + z*z );
double yang = atan2(sqrt(x*x + y*y) , z ) ;
double zang = atan2(y , x);
newx = (r*r) * sin( yang*2 + 0.5*pi ) * cos(zang*2 +pi);
newy = (r*r) * sin( yang*2 + 0.5*pi ) * sin(zang*2 +pi);
newz = (r*r) * cos( yang*2 + 0.5*pi );
Since in the standard Mandelbrot forumla, the only multiplication is the number multiplied by itself (the square), that's why there's only x, y and z in the above function, and not x2, y2, and z2 aswell. Hope that makes sense.
The addition function for these 3D numbers is as expected:
newx = x1 + x2;
newy = y1 + y2;
newz = z1 + z2;
The main Mandelbrot formula stays the same ("a" and "point" are 3D numbers of course - X, Y and Z):
add( multiply(a,a) , point).
Oh and the escape condition is slightly extended over the 2D version like so:
while (x*x + y*y + z*z < 2.0)
Thanks for doing this. It's gonna be quite exciting to see how it all turns out!
|
|
|
|
« Last Edit: November 17, 2007, 09:13:23 PM by twinbee »
|
 Logged
Logged
|
|
|
|
|
this is not kasker
Guest
|
 |
« Reply #11 on: November 17, 2007, 05:16:41 PM » |
|
This is cool, I'll be watching this thread.
|
|
|
|
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #12 on: November 17, 2007, 11:28:12 PM » |
|
heya, thanks for the formulae  just popping in to say that i'm writing my last exam for this year tomorrow, and it's a killer so there's going to be at least a 1-day lag until i implement this... oh, and you can cancel the square root / squaring for big speed gains and increased numeric stability. |
|
|
|
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #13 on: November 19, 2007, 03:51:24 AM » |
|
while sitting and staring at this thing rendering (you wouldn't believe how easily it gobbles my 12ghz of processing power), i realised i'd made a mistake in implementing the algorithm. this resulted in strange, interesting shapes:  i also think it's possible to simplify the iteration a LOT. i'm going to fix the iteration now (and also try out the "julia" version, where the constant isn't the initial point) and render it a bit while i do the algebra/trig on paper to simplify the equations. looks quite interesting so far  |
|
|
|
|
 Logged
Logged
|
|
|
|
|
lycium
|
 |
« Reply #14 on: November 19, 2007, 03:55:58 AM » |
|
i can confirm bulbs on all axes  rendering it a bit and simplifying the iteration... |
|
|
|
|
 Logged
Logged
|
|
|
|
|


















